TD N°2 : Contrôle du flux d’instructions

Ahmed Ammar (ahmed.ammar at fst.utm.tn)

Institut Préparatoire aux Études Scientifiques et Techniques, Université de Carthage.

Nov 6, 2019

Table des matières

Exercise 1: Comparer deux entiers
Exercise 2: Comparer deux chaînes
Exercise 3: Convertir Euro contre Dinar Tunisien | EUR TND
Exercise 4: Résolution d’une équation du second degré
Exercise 5: programmez une boucle while
Exercise 6: Créer une liste avec une boucle while
Exercise 7: Programmer une boucle for
Exercise 8: Ecrire une fonction Python
Exercise 9: Renvoyer trois valeurs d'une fonction Python

Exercise 1: Comparer deux entiers

Écrivez un programme qui vous demande de saisir 2 nombres entiers et affiche la plus petite de ces valeurs.

Solution.

# %load solution/ex1
valeur1= int(input("Valeur 1 : "))
valeur2= int(input("Valeur 2 : "))
if (valeur1 < valeur2 ) :
    print("Valeur la plus petite : ", valeur1)
else:
    print("Valeur la plus petite : ", valeur2)

Exercise 2: Comparer deux chaînes

Écrivez un programme qui demande d'entrer 2 chaînes et qui affiche la plus grande des 2 chaînes (celle qui contient le plus de caractères).

Solution.

# %load solution/ex2
chaine1= input("Chaîne 1 : ")
chaine2= input("Chaîne 2 : ")

if len(chaine2) > len(chaine1) :
    print ("Chaîne la plus grande : " , chaine2 )
else:
    print ("Chaîne la plus grande : " , chaine1 )

Exercise 3: Convertir Euro contre Dinar Tunisien | EUR TND

Écrivez un programme qui convertit l'euro (EUR) en dinar tunisien (TND):

Le programme commence par demander à l'utilisateur d'indiquer par une chaîne de caractères 'EUR' ou 'TND' la devise du montant qu'il entrera.
Ensuite, le programme exécute une action conditionnelle de la forme:

if devise == 'EUR' :
    # Expression 1
elif devise == 'TND' :
    # Expression 2
else :
   # affichage d'un message d'erreur

Solution.

# %load solution/ex3
devise = input("Devise : ")
montant = int(input ("Montant : "))
# 1 EUR = 3.30 TND
facteur_euro_dinar = 3.30
if devise == 'EUR' :
    print ("{} TND".format(montant * facteur_euro_dinar))

elif devise == 'TND' :
    print ("{} Euros".format(montant / facteur_euro_dinar))

else :
    print ("Je n'ai rien compris") # affichage d'un message d'erreur

Exercise 4: Résolution d’une équation du second degré

Soit l’équation du second degré $ a x^2 + bx + c = 0 $ où $ a $, $ b $ et $ c $ sont des coefficients réels.

a) Écrivez un programme qui demande d'entrer les coefficients et affiche les solutions de l'équation.

Indication.

Solutions analytiques

Des solutions sont recherchées dans le cas général, compte tenu du discriminant $ \Delta = b^2 - 4ac $, l'équation admet comme solutions analytiques: $$ \left\{ \begin{array}{ll} \Delta > 0 & deux \ solutions \ réelles : \ x_1 = \frac{-b - \sqrt{\Delta}}{2a}; \quad x_2 = \frac{-b + \sqrt{\Delta}}{2a}\\ \Delta = 0 & une \ solution \ double : \ x_0 = \frac{-b}{2a} \\ \Delta < 0 & deux \ solutions \ complexes : \ z_1 = \frac{-b - i \sqrt{-\Delta}}{2a}; \quad z_2 = \frac{-b + i \sqrt{-\Delta}}{2a} \end{array} \right. $$ Algorithme

Définition. Ensemble de règles opératoires dont l'application permet de résoudre un problème énoncé au moyen d'un nombre fini d'opérations. Un algorithme peut être traduit, grâce à un langage de programmation, en un programme exécutable par un ordinateur. Source: LAROUSSE

Pseudo-code de l'algorithme

Présentons tout d'abord un pseudo-code de l'algorithme, c'est-à-dire le détail des opérations à effectuer sans syntaxe propre du langage.

Solution.

# %load solution/ex4
"""
Calcul des racines de l'equation du second degré:
a x^2 + b x + c = 0
"""
from math import sqrt

a = float(input("Valeur de a:"))
b = float(input("Valeur de b:"))
c = float(input("Valeur de c:"))

print("L'équation a resoudre est: {} x^2 + {} x + {}".format(a,b,c))

delta = b**2 - 4*a*c  #Calcul du discriminant:

#Resultats des racines suivant la valeur de delta:
if delta > 0:
    x1 = (-b - sqrt(delta))/(2*a)
    x2 = (-b + sqrt(delta))/(2*a)
    # Affichage des solutions trouvées
    print("Les solutions sont réelles: ")
    print("La premiere racine est x1= ",x1)
    print("La seconde racines est x2= ",x2)

elif delta == 0:
    x0 = -b/(2*a)
    # Affichage de la solution trouvée
    print("Il y a une seule solution: ")
    print("La solution est", x0)

elif delta<0:
    z1 = (-b - 1j*sqrt(-delta))/(2*a)
    z2 = (-b + 1j*sqrt(-delta))/(2*a)
    # Affichage des solutions trouvées
    print("Les solutions sont complexes: ")
    print("La premiere racine est z1 = ", z1)
    print("La seconde racine est z2 = ", z2)

b) Soit la fonction $ f(x) = 0.83 x^2 + 3.8 x + 2.48 $. En utilisant le programme précédent, trouvez les solutions pour $ f(x) = 0 $.

Solution.

Les solutions des $ f(x) = 0 $ sont réelles: $ x_1 = $ et $ x_2 = $

c) La représentation graphique de $ f(x) $ est indiquée ci-dessous:

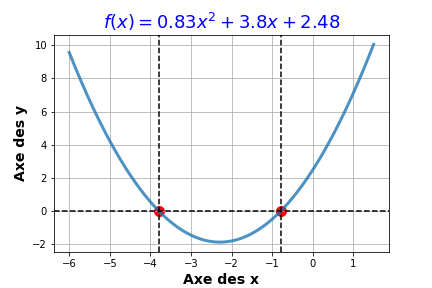
Nous allons utiliser une fonction EqSecondDegree(a,b,c) dans TD N°3 pour reproduire cette figure en utilisant les bibliothèques numpy et matplotlib.

Écrivez la fonction EqSecondDegree(a,b,c) qui renvoie les solutions de l'équation $ a x^2 + bx + c = 0 $.
Enregistrez la fonction EqSecondDegree(a,b,c) dans un script Python racines.py.

Solution.

# %load racines.py
def EqSecondDegree(a,b,c):
    """
    Calcul des racines de l'equation du second degré:
    a x^2 + b x + c = 0
    """
    from math import sqrt

    print("L'équation a resoudre est: {} x^2 + {} x + {}".format(a,b,c))

    delta = b**2 - 4*a*c  #Calcul du discriminant:

    #Resultats des racines suivant la valeur de delta:
    if delta > 0:
        x1 = (-b - sqrt(delta))/(2*a)
        x2 = (-b + sqrt(delta))/(2*a)
        # Affichage des solutions trouvées
        print("Les solutions sont réelles: ")
        print("La premiere racine est x1= ",x1)
        print("La seconde racines est x2= ",x2)
        return x1, x2

    elif delta == 0:
        x0 = -b/(2*a)
        # Affichage de la solution trouvée
        print("Il y a une seule solution: ")
        print("La solution est", x0)
        return x0

    elif delta<0:
        z1 = (-b - 1j*sqrt(-delta))/(2*a)
        z2 = (-b + 1j*sqrt(-delta))/(2*a)
        # Affichage des solutions trouvées
        print("Les solutions sont complexes: ")
        print("La premiere racine est z1 = ", z1)
        print("La seconde racine est z2 = ", z2)
        return z1, z2

# Exécutez le scripte racines.py
EqSecondDegree(a=0.83,b=3.8,c=2.48)

d) En utilisant la fonction EqSecondDegree(a,b,c), trouvez les solutions de $ f(x) = 0 $.

Solution.

from racines import EqSecondDegree
x1, x2 = EqSecondDegree(0.83,3.8,2.48)
print("x1 = {:.3f} et x2 = {:.3f}".format(x1, x2))

Exercise 5: programmez une boucle `while`

Définir une séquence de nombres: $$x_n = n^2 + 1$$

pour les entiers n = 0,1,2,…, N. Écrivez un programme qui affiche $ x_n $ pour n = 0,1,…, 20 en utilisant une boucle while.

Solution.

Le programme qui affiche $ x_n $ pour n = 0,1,…, 20 en utilisant une boucle while s'écrit:

n = 0
while n <= 20:
    x_n = n**2 + 1
    print('x{} = {}'.format(n, x_n))
    n = n + 1

Exercise 6: Créer une liste avec une boucle `while`

Stockez toutes les valeurs $ x_n $ calculées dans l'exercice 5 dans une liste (à l'aide d'une boucle while). Afficher la liste complète (en un seul objet).

Solution.

Les valeurs $ x_n $ sont stockés dans une liste x définie:

n = 0
x = []  # les x_n valeurs
while n <= 20:
    x.append(n**2 + 1)
    n = n + 1
print(x)

Exercise 7: Programmer une boucle `for`

Faites l'exercice 6, mais utilisez une boucle for.

Solution.

Le programme avec une boucle for s'écrit:

# %load solution/ex7
x = []
for n in range(21):
    x.append(n**2 + 1)
print(x)

On peut également raccourcir le code en utilisant une liste de compréhension:

print([n**2 +1 for n in range(21)])

Exercise 8: Ecrire une fonction Python

Écrivez une fonction x(n) pour calculer un élément dans la séquence $ x_n = n^2 + 1 $. Appelez la fonction pour n = 4 et afficher le résultat.

Solution.

La fonction x(n) est définie:

def x(n):
    return n**2 +1
print(x(4))

Exercise 9: Renvoyer trois valeurs d'une fonction Python

Écrivez une fonction Python qui évalue les fonctions mathématiques $ f(x) = cos(2x) $, $ f'(x) = -2sin(2x) $ et $ f"(x) = - 4 cos(2x) $. Retourner ces trois valeurs. Écrivez les résultats de ces valeurs pour $ x = \pi $.

Solution.

Soit une fonction deriv2(x) qui renvoie les valeurs de $ f(x) $, $ f'(x) $ et $ f"(x) $:

from math import sin, cos, pi

def deriv2(x):
    return cos(2*x), -2*sin(2*x), -4*cos(2*x)

f, df, d2f = deriv2(x=pi)

print("f(pi) = {}; df(pi) = {}; d2f(pi) = {} ".format(f, df, d2f))

TD N°2 : Contrôle du flux d’instructions

Nov 6, 2019

Table des matières

Exercise 1: Comparer deux entiers

Exercise 2: Comparer deux chaînes

Exercise 3: Convertir Euro contre Dinar Tunisien | EUR TND

Exercise 4: Résolution d’une équation du second degré

Exercise 5: programmez une boucle while

Exercise 6: Créer une liste avec une boucle while

Exercise 7: Programmer une boucle for

Exercise 8: Ecrire une fonction Python

Exercise 9: Renvoyer trois valeurs d'une fonction Python

Exercise 5: programmez une boucle `while`

Exercise 6: Créer une liste avec une boucle `while`

Exercise 7: Programmer une boucle `for`