TD N°5 : Équations différentielles ordinaires

Ahmed Ammar (ahmed.ammar at fst.utm.tn)

Institut Préparatoire aux Études Scientifiques et Techniques, Université de Carthage.

Mar 10, 2020

Table des matières

Exercice 1: Pendule simple
Exercice 2: Comparaison des schémas d’Euler explicite et implicite
Exercice 3: Atterrissage d'un vaisseau spatial

Exercice 1: Pendule simple

On considère un pendule simple de masse $ m =1 \ kg $ , de longueur $ l=1 \ m $ qui va osciller d’arrière en avant à cause du champ de gravité de la Terre $ g = 9.8 \ m/s^2 $.

Le pendule a l'équation du mouvement : $$ \begin{align} \ddot{\theta} &= - \frac{g}{l} sin(\theta) \label{_auto1} \end{align} $$ Pour les petites amplitudes d'oscillation, $ \theta \ll 1 $, on peut faire l'approximation $ sin(\theta) \approx \theta $, on retrouve alors l’équation différentielle d’un oscillateur harmonique: $$ \begin{align} \label{eq:eqdiff} \ddot{\theta} &= - \frac{g}{l} \theta \end{align} $$

La solution exacte de cette équation est simplement: $$ \begin{align} \label{eq:solexacte} \theta (t) &= \theta_0 \ cos(\omega_0 t) \end{align} $$ où $ \omega_0 = \sqrt{g/l} $ et nous avons supposé que le pendule partait du repos avec un déplacement initial $ \theta_0 =0.2 \ rad $.

Nous allons transformer l'équation différentielle d’ordre 2 (Eq. \eqref{eq:eqdiff}) en deux équations différentielles d’ordre 1 afin de pouvoir utiliser simplement la méthode d’Euler. En posant $ \omega (t)= \dot{\theta}(t) $ la vitesse angulaire du pendule, on obtient le système de deux fonctions inconnues suivant : $$ \begin{align} \dot{\theta} (t) &= \omega (t) \label{_auto2}\\ \dot{\omega }(t) &= - \omega_0^2 \ \theta (t) \label{_auto3} \end{align} $$ Pour résoudre ce système nous devons connaître les deux conditions initiales suivantes : $$ \begin{align*} \theta(0) &= \theta_0 \\ \omega (0) &= 0 \end{align*} $$

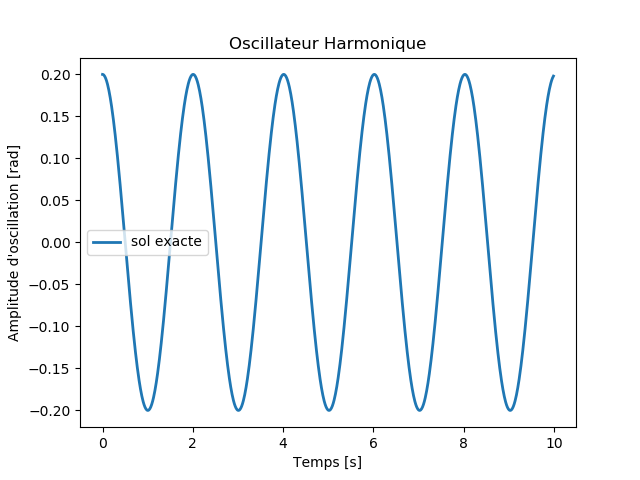
a) Définir une fonction sol_exacte(t) qui renvoie la solution exacte de l'oscillateur harmonique donnée par l'équation \eqref{eq:solexacte}. Tracer cette solution pour $ t \in [0,10] $ et pour un pas de $ \Delta t = 0.01 $ s.

Indication.

Utiliser la fonction numpy.arange() pour créer le vecteur temps t.
Utiliser la fonction matplotlib.pyplot.plot() pour tracer sol_exacte(t).

Solution.

Le programme Python qui renvoie et trace la solution exacte de l'oscillateur harmonique est le suivant:

import numpy as np
import matplotlib.pyplot as plt
# SYSTÈME: PENDULE SIMPLE
g = 9.8 # accélération de pesanteur [m/s^2]
l = 1 # longeur du pendule [m]
dt = 0.01 # pas du temps [s]
Tf = 10 # temps finale de la simulation [s]
theta0 = 0.2 # angle initiale [rad]
omega0 = np.sqrt(g/l) 
# SOLUTION EXACTE
def pendule_exacte(t):
    return theta0 * np.cos(omega0 * t)
t = np.arange(0, Tf, dt)

plt.plot(t, pendule_exacte(t), linewidth=2, label="sol exacte")
plt.legend()
plt.ylabel("Amplitude d'oscillation [rad]")
plt.xlabel("Temps [s]")
plt.title("Oscillateur Harmonique")
plt.show()

L'exécution de ce programme donne la figure suivante:

b) Rappeler l'expression de la méthode d'Euler explicite pour ce système.

Solution.

$$ \begin{align} \label{eq:euler_exp} \pmb{u}_{k+1} &= \pmb{u}_k + \Delta t \pmb{A} \cdot \pmb{u}_k = (\pmb{I} + \Delta t \pmb{A}) \cdot \pmb{u}_k \end{align} $$

Où $ \pmb{u}_k= \left(\begin{array}{c} \theta_k \\ \omega_k \end{array}\right) $, $ \pmb{A}= \left(\begin{array}{ll} 0&1 \\ - g/l& 0 \end{array}\right) $ et $ \pmb{I} $ est la matrice identité.

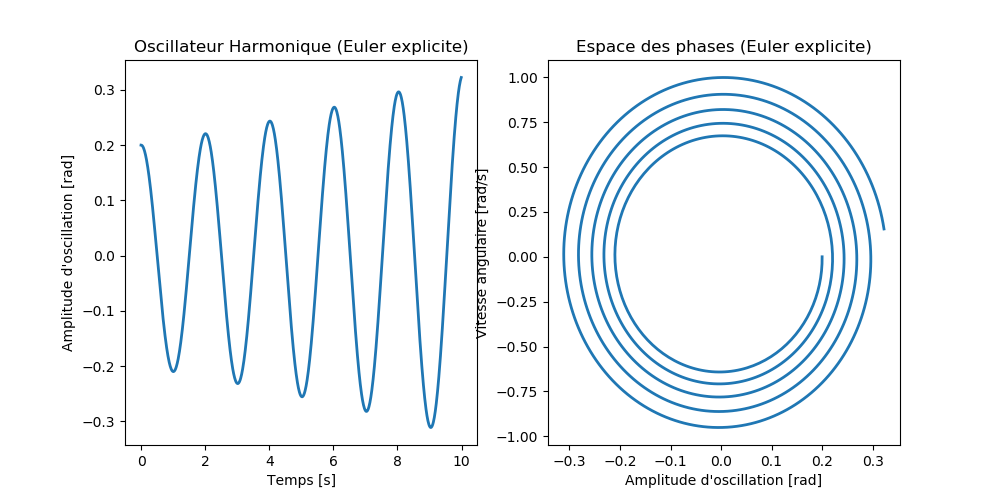
c) Calculer $ \pmb{u}= \left(\begin{array}{c} \theta (t) \\ \omega (t) \end{array}\right) $ avec la méthode d'Euler explicite pour $ t \in [0, 10] $ et pour un pas d’intégration $ \Delta t = 0.01 $ s.

Tracer:

Dans un même graphique, la variation de l'amplitude d'oscillation $ \theta $ en fonction du temps $ t $ et le diagramme des phases (vitesse angulaire $ \omega $ en fonction de $ \theta $).
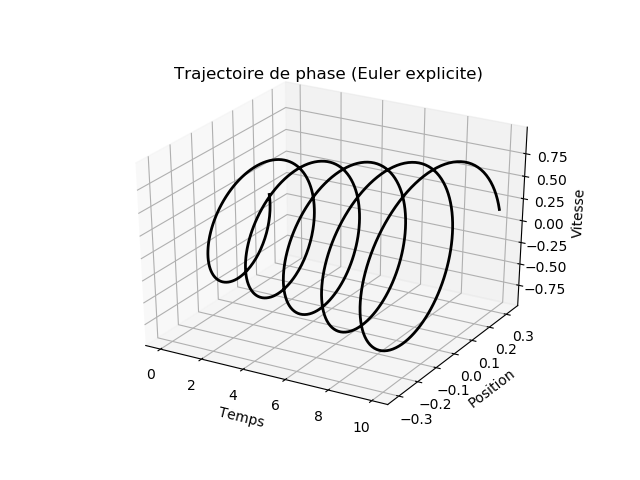
Dans un graphique 3D, la vitesse angulaire $ \omega $ et l'amplitude d'oscillation $ \theta $ en fonction du temps $ t $.

Que remarquez-vous pour le résultat trouvé?

Indication.

On vous donne les instructions nécessaires pour reproduire un graphique en 3D:

from mpl_toolkits.mplot3d.axes3d import Axes3D
plt.figure()
ax = plt.axes(projection="3d")
ax.plot(....)

Solution.

#%% EULER EXPLICITE
A = np.array([[0, 1], [- omega0**2, 0]])
nsteps = int(Tf/dt)
# CONDITIONS INITIALES: à t = 0; theta = theta0, omega = 0
u0 = np.array([theta0, 0])

Texp = np.zeros(nsteps)
Uexp = np.zeros((2, nsteps))
Texp[0] = 0.0
Uexp[:,0] = u0
# ITÉRATION
for k in range(nsteps-1):
    Texp[k+1] = Texp[k] + dt
    Uexp[:,k+1] = np.dot((np.eye(2) + dt * A), Uexp[:,k])
    
plt.figure(figsize=(10,5))
# PLOT POSITION vs TEMPS
plt.subplot(1,2,1)
plt.plot(Texp,Uexp[0,:], linewidth=2)
plt.xlabel("Temps [s]")
plt.ylabel("Amplitude d'oscillation [rad]")
plt.title("Oscillateur Harmonique (Euler explicite)")
# DIAGRAMME DE PHASE 2D
plt.subplot(1,2,2)
plt.plot(Uexp[0,:],Uexp[1,:], linewidth=2)
plt.xlabel("Amplitude d'oscillation [rad]")
plt.ylabel("Vitesse angulaire [rad/s]")
plt.title("Espace des phases (Euler explicite)")
plt.savefig("Pendule_EulerExp1D.png"); plt.savefig("Pendule_EulerExp1D.pdf")
# DIAGRAMME DE PHASE 3D
from mpl_toolkits.mplot3d.axes3d import Axes3D
plt.figure()
ax = plt.axes(projection="3d")
ax.plot(Texp, Uexp[0,:],Uexp[1,:], linewidth=2)
ax.set_xlabel("Temps [s]")
ax.set_ylabel("Amplitude d'oscillation [rad]")
ax.set_zlabel("Vitesse angulaire [rad/s]")
ax.set_title("Espace des phases (Euler explicite)")
plt.show()

L'exécution de ce programme donne les figures suivantes:

et la figure en 3D:

Remarque. Dans le cas d'intégration avec la méthode d'Euler explicite nous avons un problème d’augmentation d’amplitude dans le cas d’un oscillateur libre non amorti. Plus le temps de simulation est long, plus l'amplitude augmente, ce qui n'est pas ce que nous attendons de l'évolution du système dans le temps.

d) Rappeler l'expression de la méthode d'Euler implicite pour ce système.

Solution.

$$ \begin{align} \label{eq:euler_imp} \pmb{u}_{k+1} &=(\pmb{I} - \Delta t \pmb{A})^{-1} \cdot \pmb{u}_k \end{align} $$

e) Calculer $ \pmb{u}= \left(\begin{array}{c} \theta (t) \\ \omega (t) \end{array}\right) $ avec la méthode d'Euler implicite pour $ t \in [0, 10] $ et pour un pas d'integration $ \Delta t = 0.01 $ s.

Tracer:

Dans un même graphique, la variation de l'amplitude d'oscillation $ \theta $ en fonction du temps $ t $ et le diagramme des phases (vitesse angulaire $ \omega $ en fonction de $ \theta $).
Dans un graphique 3D, la vitesse angulaire $ \omega $ et l'amplitude d'oscillation $ \theta $ en fonction du temps $ t $.

Que remarquez-vous pour le résultat trouvé?

Solution.

#%% EULER IMPLICITE
from numpy.linalg import inv
Timp = np.zeros(nsteps)
Uimp = np.zeros((2, nsteps))
Timp[0] = 0.0
Uimp[:,0] = u0
# ITÉRATION
for k in range(nsteps-1):
    Timp[k+1] = Timp[k] + dt
    Uimp[:,k+1] = np.dot(inv(np.eye(2) - dt * A), Uimp[:,k])
    
plt.figure(figsize=(10,5))
# PLOT POSITION vs TEMPS
plt.subplot(1,2,1)
plt.plot(Timp,Uimp[0,:], linewidth=2)
plt.xlabel("Temps [s]")
plt.ylabel("Amplitude d'oscillation [rad]")
plt.title("Oscillateur Harmonique (Euler implicite)")
# DIAGRAMME DE PHASE
plt.subplot(1,2,2)
plt.plot(Uimp[0,:],Uimp[1,:], linewidth=2)
plt.xlabel("Amplitude d'oscillation [rad]")
plt.ylabel("Vitesse angulaire [rad/s]")
plt.title("Espace des phases (Euler implicite)")
plt.savefig("Pendule_Eulerimp1D.png"); plt.savefig("Pendule_Eulerimp1D.pdf")
plt.show()
# DIAGRAMME DE PHASE 3D
plt.figure()
ax = plt.axes(projection="3d")
ax.plot(Timp, Uimp[0,:],Uimp[1,:], linewidth=2)
ax.set_xlabel("Temps [s]")
ax.set_ylabel("Amplitude d'oscillation [rad]")
ax.set_zlabel("Vitesse angulaire [rad/s]")
ax.set_title("Espace des phases (Euler implicite)")
plt.savefig("Pendule_Eulerimp3D.png"); plt.savefig("Pendule_Eulerimp3D.pdf")
plt.show()

L'exécution de ce programme donne les figures suivantes:

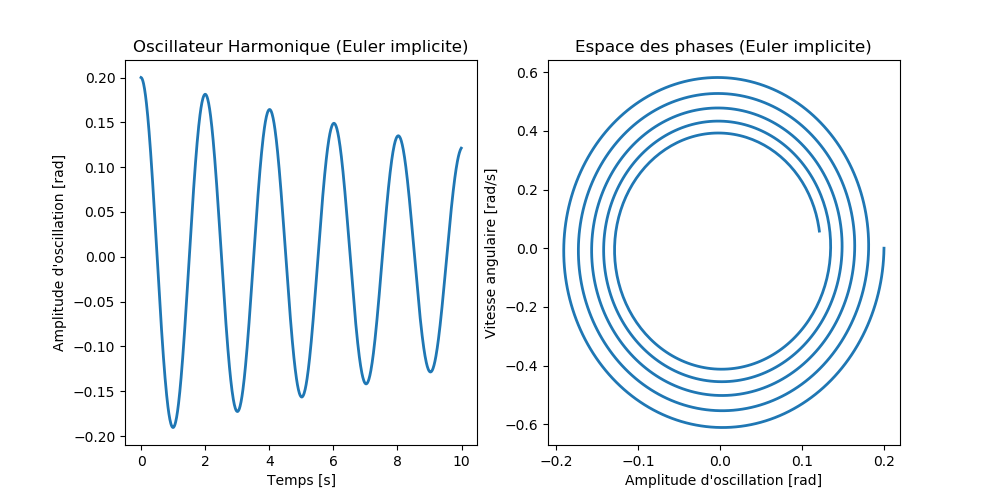
et la figure en 3D:

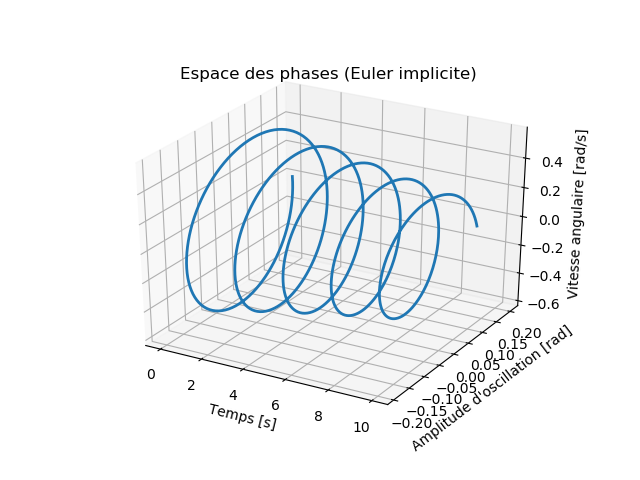
Remarque. Dans le cas d'intégration avec la méthode d'Euler implicite nous avons un problème de diminution d’amplitude dans le cas d’un oscillateur libre non amorti. Plus le temps de simulation est long, plus l'amplitude diminue, ce qui n'est pas ce que nous attendons de l'évolution du système dans le temps.

f) Tracer dans un même graphique pour $ t \in [0, 10] $ et avec un pas $ \Delta t = 0.01 $ s:

sol_exacte(t) calculée dans a).
$ \theta (t) $ calculée dans c) par la méthode d'Euler explicite.
$ \theta (t) $ calculée dans e) par la méthode d'Euler implicite.

Que remarquez-vous si nous modifions la valeur du pas d’intégration par $ \Delta t =~0.001 $ s? Expliquer le résultat trouvé.

Solution.

#%% ILLUSTRATION
plt.figure()
plt.plot(t, pendule_exacte(t), linewidth=2, label="sol exact")
plt.plot(t, Uexp[0,:], linewidth=2, linestyle='--', label="Euler explicite")
plt.plot(t, Uimp[0,:], linewidth=2, linestyle='--', label="Euler implicite")
plt.legend()
plt.xlabel("Temps [s]")
plt.ylabel("Amplitude d'oscillation [rad]")
plt.title("Oscillateur Harmonique avec "+ r"$\Delta t =$"+str(dt))
plt.savefig("Pendule_illustration.png"); plt.savefig("Pendule_illustration.pdf")
plt.show()

Pour $ \Delta t = 0.01 $, l'exécution du code donne la figure suivante:

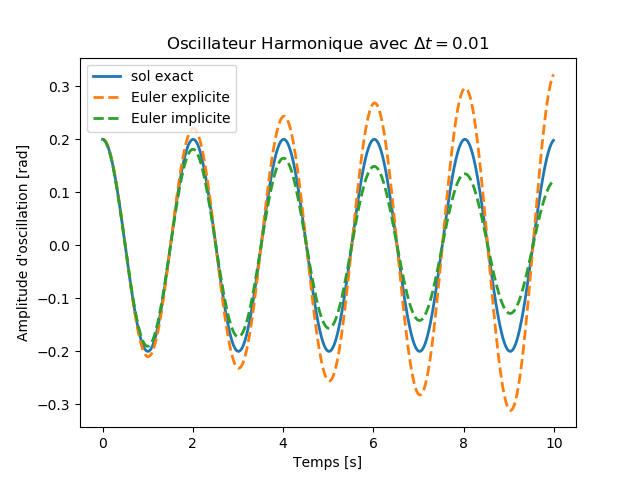
Pour $ \Delta t = 0.001 $, l'exécution du code donne la figure suivante:

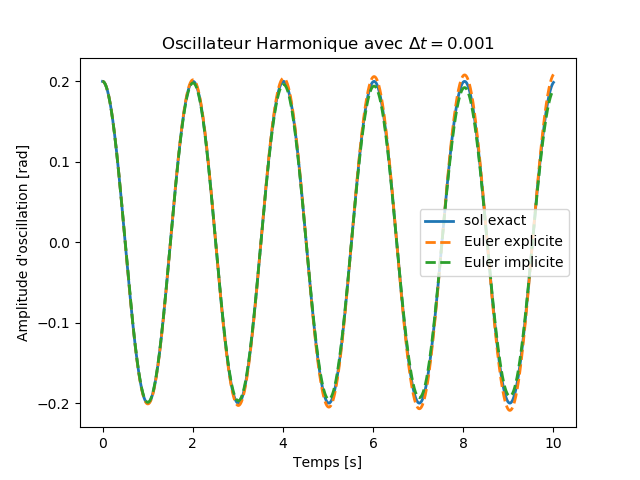
Remarque. Les deux méthodes d'Euler, explicite et implicite, posent un problème fondamental avec ses amplitudes croissantes et décroissantes pour le cas d'oscillateur libre non amorti. Un très petit $ \Delta t $ est nécessaire pour obtenir des résultats satisfaisants.

Plus la simulation est longue, plus $ \Delta t $ doit être petit.

Exercice 2: Comparaison des schémas d’Euler explicite et implicite

On considère le problème de Cauchy: $$ \begin{align} \label{eq:equdiffEx2} \frac{d z(t)}{dt} = 1 - \frac{t}{\mu}, \ t \in \Re, \ z(0) = z_0 \end{align} $$ On rappelle que la solution exacte de ce problème est donnée par: $$ \begin{align} \label{eq:solexacte2} z(t) = \mu -(\mu - z_0) e^{-\frac{t}{\mu}} \end{align} $$

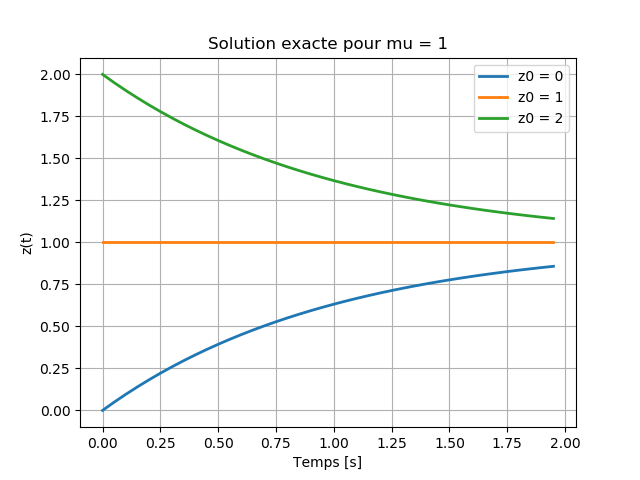
a) Définir une fonction sol_exacte(t, mu, z0) qui renvoie la solution exacte donnée par l'équation \eqref{eq:solexacte2}. Tracer sur un même graphique pour $ \mu= 1 $ et $ z_0 \in \{0, 1, 2\} $ ces solutions. Soit $ t \in [0,2] $ et pour un pas de $ \Delta t = 0.1 $ s.

Solution.

Voir la partie qui commence par #Question-a) dans le code Python à la fin de l'exercice.
La figure ci-dessous est la sortie de cette partie du code:

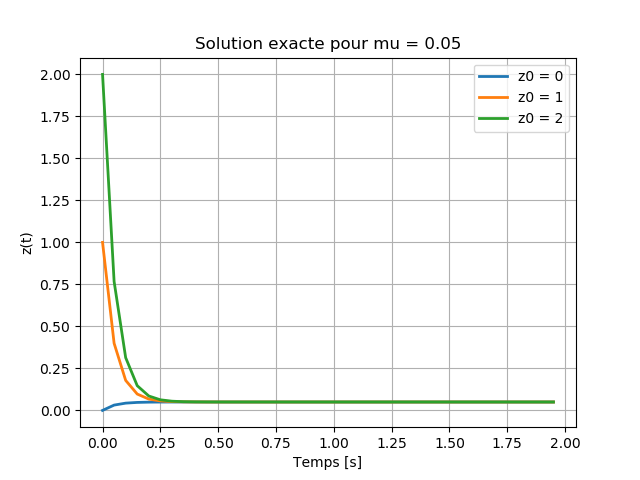
b) Même questions pour $ \mu= 0.05 $ et $ z_0 \in \{0, 1, 2\} $.

Solution.

Voir la partie qui commence par #Question-b) dans le code Python à la fin de l'exercice.
La figure ci-dessous est la sortie de cette partie du code:

On suppose dans cette question que $ \mu= 0.05 $ et que $ z_0 = 2 $. c) Rappeler l'expression de la méthode d'Euler explicite pour ce problème. Calculer $ z(t) $ avec la méthode d’Euler explicite pour $ t \in [0, 2] $ et pour un pas d’intégration $ \Delta t = 0.1 $ s.

Solution.

L'expression de la méthode d'Euler explicite sous sa forme scalaire s'écrit: $$\frac{z_{n+1} - z_n}{\Delta t} = \dot{z_n} = f(z_n)$$ Or d'après l'équation \eqref{eq:equdiffEx2} nous avons $ f(z_n) = 1 - \frac{z_n}{\mu} $, d'où le schémas explicite d'Euler: $$z_{n+1} = z_n + \Delta t (1 - \frac{z_n}{\mu}) , \ n = 0, 1, 2, ..., N-1.$$

Voir la partie qui commence par #Question-c) - EULER EXPLICITE dans le code Python à la fin de l'exercice.

d) Montrer que l'expression de la méthode d'Euler implicite est: $$z_{n+1} = \frac{z_n + \Delta t}{1 + \frac{\Delta t}{\mu}}, \ n = 0, 1, 2, ..., N-1.$$ Calculer $ z(t) $ avec la méthode d'Euler implicite pour $ t \in [0, 2] $ et pour un pas d’intégration $ \Delta t = 0.1 $ s.

Solution.

L'expression de la méthode d'Euler implicite sous sa forme scalaire s'écrit: $$\frac{z_{n+1} - z_n}{\Delta t} = \dot{z_n} = f(z_{n+1})$$ Or d'après l'équation \eqref{eq:equdiffEx2} nous avons $ f(z_{n+1}) = 1 - \frac{z_{n+1}}{\mu} $, par la suite : $$z_{n+1} = z_n + \Delta t (1 - \frac{z_{n+1}}{\mu})$$ d'où le schémas implicite d'Euler: $$z_{n+1} = \frac{z_n + \Delta t}{1 + \frac{\Delta t}{\mu}}, \ n = 0, 1, 2, ..., N-1.$$

Voir la partie qui commence par #Question-d) - EULER IMPLICITE dans le code Python à la fin de l'exercice.

e) Tracer dans un même graphique pour $ t \in [0, 2] $ et avec des pas d'intégration $ \Delta t = 0.5, 0.1, 0.05, 0.01, 0.005 $ s:

La solution exacte: sol_exacte(t, 0.05, 2)
$ z(t) $ calculée par la méthode d'Euler explicite.
$ z(t) $ calculée par la méthode d'Euler explicite.

Que remarquez-vous pour les résultats trouvés? Quelle est la méthode la plus proche de la solution exacte?

Solution.

La figure ci-dessous illustre l'importance du choix du pas d'intégration $ \Delta t $ pour obtenir une bonne approximation de la solution exacte.

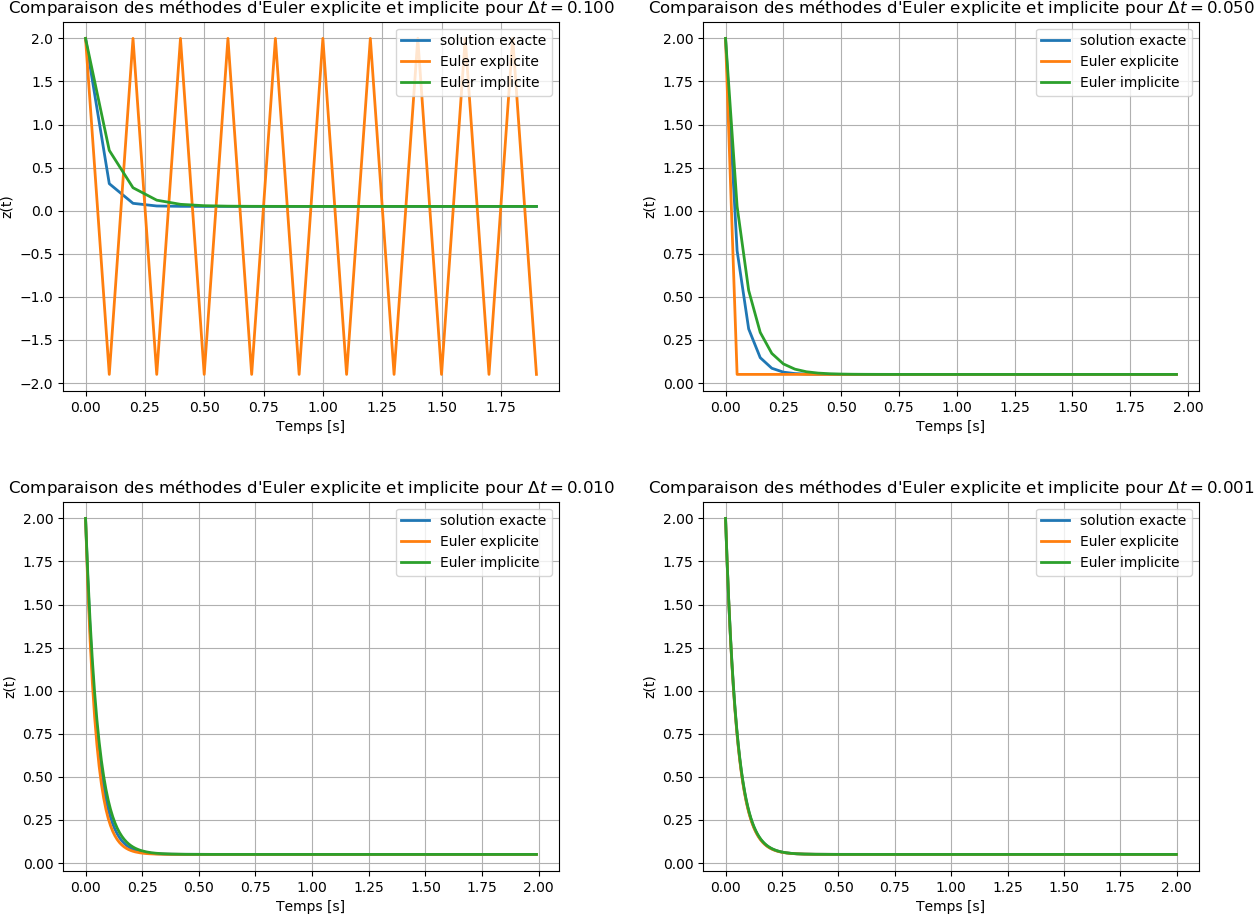
pour $ \Delta t = 0.5 $ : Peu de points pour juger la stabilité des méthodes.
pour $ \Delta t = 0.1 $ : Le schéma d'Euler implicite donne une meilleure approximation tandis que le schéma explicite montre un instabilité figuré par des oscillations autour de la solution exacte exacte.
pour $ \Delta t = 0.01 $ : Les deux schémas donnent assez bonnes approximations. La solution exacte se trouve au milieu des solutions implicites et explicites.
pour $ \Delta t = 0.001 $ : Les deux schémas donnent des solutions qui sont maintenant confondues avec la solution exacte alors que le temps de calcul devient relativement important!

En conclusion, le schéma d'Euler implicite est beaucoup plus stable que le schéma explicite et donne toujours une bonne approximation.

Le code Python pour cet exercice est le suivant:

## NOM DU PROGRAMME: EulerEx2.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
#Question-a)
def sol_exacte(t, mu, z0):
    return mu - (mu-z0)* np.exp(-t/mu)

mu = 1
z0 = [0, 1, 2]
dt = 0.05
t = np.arange(0, 2, dt)
plt.figure()
for zi in z0:
    plt.plot(t, sol_exacte(t, mu, zi),lw = 2, label= "z0 = " + str(zi))
plt.title("Solution exacte pour mu = 1")
plt.xlabel("Temps [s]")
plt.ylabel("z(t)")
plt.legend()
plt.grid()
plt.savefig("Ex2_solexactemu1.png");plt.savefig("Ex2_solexactemu1.pdf")
plt.show()
#Question-b)
mu = 0.05
plt.figure()
for zi in z0:
    plt.plot(t, sol_exacte(t, mu, zi), lw = 2, label= "z0 = " + str(zi))
plt.title("Solution exacte pour mu = 0.05")
plt.xlabel("Temps [s]")
plt.ylabel("z(t)")
plt.legend()
plt.grid()
plt.savefig("Ex2_solexactemu005.png");plt.savefig("Ex2_solexactemu005.pdf")
plt.show()
#Question-c) - EULER EXPLICITE
z0 = 2
N = len(t)
zexp =np.zeros(N)
zexp[0] = z0
for n in range(N-1):
    zexp[n+1] = zexp[n] + dt*(1- zexp[n]/mu)

#Question-d) - EULER IMPLICITE
zimp =np.zeros(N)
zimp[0] = z0
for n in range(N-1):
    zimp[n+1] = (zimp[n] + dt)/(1+ dt/mu)
#Question-e) - COMPARAISON
plt.figure()
plt.plot(t, sol_exacte(t, mu, z0), lw = 2, label= "solution exacte")
plt.plot(t, zexp, lw = 2, label= "Euler explicite")
plt.plot(t, zimp, lw = 2, label= "Euler implicite")
plt.xlabel("Temps [s]")
plt.ylabel("z(t)")
plt.legend()
plt.grid()
plt.show()

Exercice 3: Atterrissage d'un vaisseau spatial

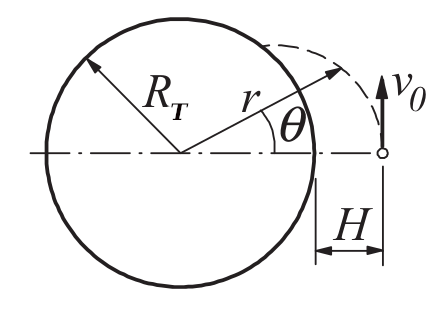
Un vaisseau spatial est lancé à l'altitude $ H = 772 \ km $ au-dessus du niveau de la mer avec la vitesse $ v_0 = 6700 \ m/s $ dans la direction indiquée sur la figure ci-dessus. Les équations différentielles décrivant le mouvement du vaisseau spatial sont: $$ \begin{align*} \ddot{r} &= r \dot{\theta}^2 - \frac{G M_T}{r^2} \\ \ddot{\theta} &= - \frac{2 \dot{r} \dot{\theta}}{r} \end{align*} $$ où $ r $ et $ \theta $ sont les coordonnées polaires du vaisseau spatial. Les constantes impliquées dans le mouvement sont:

$ G = 6.672 \times 10^{−11} \ m^3 kg^{−1} s^{−2} $ = constante gravitationnelle universelle.
$ M_T = 5.9742 \times 10^{24} \ kg $ = masse de la terre.
$ R_T = 6378.14 \ km $ = rayon de la terre au niveau de la mer.

a) Dériver les équations différentielles du premier ordre et les conditions initiales de la forme $ \dot{y} = F (t, y) $, $ y(0) = b $.

Solution.

Nous avons: $$ G M_T = (6.672 \times 10^{-11}) \ (5.9742 \times 10^{24}) = 3.9860 \times 10^{14} \ m^3/s^2 $$ Soit: $$ y = \left[\begin{array}{c} y_0 \\ y_1 \\ y_2 \\ y_3 \end{array}\right] = \left[\begin{array}{c} r \\ \dot{r} \\ \theta \\ \dot{\theta} \end{array}\right]$$ Les équations équivalentes du premier ordre deviennent: $$F(t, y) = \left[\begin{array}{c} \dot{y_0} \\ \dot{y_1} \\ \dot{y_2} \\ \dot{y_3} \end{array}\right] = \left[\begin{array}{c} y_1 \\ y_0 y_3^2 - 3.9860 \times 10^{14}/y_0^2 \\ y_3 \\ -2 y_1 y_3/y_0 \end{array}\right]$$ et les conditions initiales sont: $$ \begin{align*} r(0) &= R_T + H = (6378.14 + 772) \times 10^{3} = 7.15014 \times 10^{6} \ m \\ \dot{r}(0) &= 0 \\ \theta (0) &= 0 \\ \dot{\theta}(0) &= v_0/r(0) = (6700)/(7.15014 \times 10^6) = 0.937045 \times 10^{-3} \ rad/s \end{align*} $$ Ainsi, $$ y = \left[\begin{array}{c} 7.15014 \times 10^{6} \\ 0 \\ 0 \\ 0.937045 \times 10^{-3} \end{array}\right]$$

b) Utiliser la méthode Runge-Kutta du quatrième ordre (RK4) pour intégrer les équations depuis le lancement jusqu'à ce que le vaisseau spatial touche la terre. Déterminez $ \theta $ au site d'impact.

Solution.

Le code Python est le suivant:

## NOM DU PROGRAMME: RK4Ex3.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
def RK4(F,t,y,h):
    K0 = h*F(t,y)
    K1 = h*F(t + h/2.0, y + K0/2.0)
    K2 = h*F(t + h/2.0, y + K1/2.0)
    K3 = h*F(t + h, y + K2)
    return (K0 + 2.0*K1 + 2.0*K2 + K3)/6.0
def F(t,y):
    F = np.zeros(4)
    F[0] = y[1]
    F[1] = y[0]*(y[3]**2) - 3.9860e14/(y[0]**2)
    F[2] = y[3]
    F[3] = -2.0*y[1]*y[3]/y[0]
    return F
t = 0
tStop = 1200.0
h = 50.0
y = np.array([7.15014e6, 0.0, 0.0, 0.937045e-3])
T = []
Y = []
T.append(t)
Y.append(y)
while t < tStop:
    y = y + RK4(F,t,y,h)
    t = t + h
    T.append(t)
    Y.append(y)
    
T,Y = np.array(T),np.array(Y)
print("T      Y[0]       Y[1]      Y[2]       Y[3]")
for i in range(len(T)):
    print(T[i], "{:2.4e}".format(Y[i,0]), "{:2.4e}".format(Y[i,1]),
          "{:2.4e}".format(Y[i,2]), "{:2.4e}".format(Y[i,3]))
    
plt.figure(figsize=(8,5))
plt.plot(T, Y[:,0], '-o',lw = 2)
plt.xlabel("temps [s]")
plt.ylabel("r [m]")
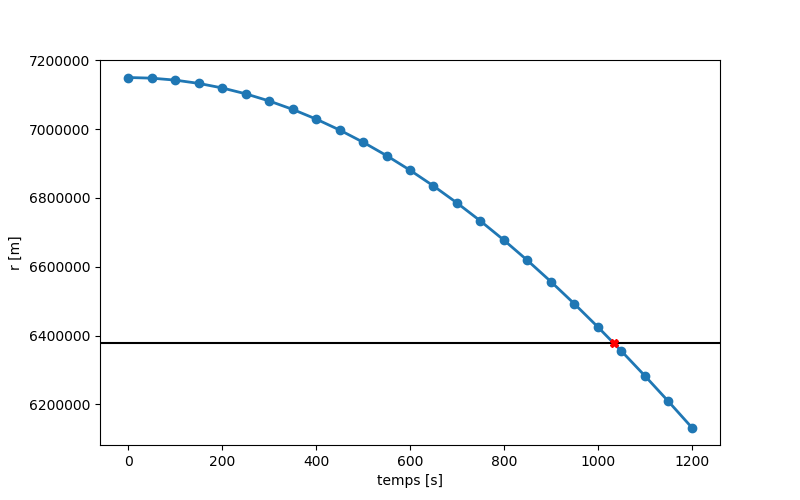
plt.axhline(y=6.37814E6, color="k")
# plot point d'impact
plt.plot(1034.184,6.37814E6,'rX')
plt.savefig("Ex3RK4.png"); plt.savefig("Ex3RK4.pdf")
plt.show()

La sortie du programme est :

T      Y[0]       Y[1]      Y[2]       Y[3]
0.0 7.1501e+06 0.0000e+00 0.0000e+00 9.3704e-04
50.0 7.1482e+06 -7.5908e+01 4.6861e-02 9.3754e-04
100.0 7.1426e+06 -1.5173e+02 9.3771e-02 9.3904e-04
150.0 7.1331e+06 -2.2738e+02 1.4078e-01 9.4153e-04
200.0 7.1198e+06 -3.0276e+02 1.8794e-01 9.4504e-04
250.0 7.1028e+06 -3.7779e+02 2.3530e-01 9.4958e-04
300.0 7.0820e+06 -4.5236e+02 2.8292e-01 9.5515e-04
350.0 7.0576e+06 -5.2638e+02 3.3084e-01 9.6179e-04
400.0 7.0294e+06 -5.9973e+02 3.7911e-01 9.6951e-04
450.0 6.9976e+06 -6.7229e+02 4.2780e-01 9.7834e-04
500.0 6.9622e+06 -7.4393e+02 4.7697e-01 9.8832e-04
550.0 6.9232e+06 -8.1452e+02 5.2666e-01 9.9947e-04
600.0 6.8808e+06 -8.8389e+02 5.7693e-01 1.0118e-03
650.0 6.8349e+06 -9.5189e+02 6.2786e-01 1.0255e-03
700.0 6.7856e+06 -1.0183e+03 6.7950e-01 1.0404e-03
750.0 6.7331e+06 -1.0830e+03 7.3193e-01 1.0567e-03
800.0 6.6773e+06 -1.1456e+03 7.8520e-01 1.0744e-03
850.0 6.6185e+06 -1.2060e+03 8.3940e-01 1.0936e-03
900.0 6.5568e+06 -1.2639e+03 8.9459e-01 1.1143e-03
950.0 6.4922e+06 -1.3189e+03 9.5085e-01 1.1366e-03
1000.0 6.4250e+06 -1.3708e+03 1.0083e+00 1.1605e-03
1050.0 6.3552e+06 -1.4191e+03 1.0669e+00 1.1861e-03
1100.0 6.2831e+06 -1.4634e+03 1.1269e+00 1.2135e-03
1150.0 6.2089e+06 -1.5034e+03 1.1883e+00 1.2427e-03
1200.0 6.1329e+06 -1.5384e+03 1.2512e+00 1.2737e-03

Le vaisseau spatial frappe la terre lorsque r est égal à $ R_T = 6.37814 \times 10^6 \ m $. Cela se produit entre $ t = 1000 $ et $ 1050 $ s. Laissant $ 1000 + \Delta t $ être le moment de l'impact, nous pouvons écrire: $$r(1000 + \Delta t ) = R_T$$ En développant $ r $ dans une série Taylor à deux termes, nous obtenons: $$r(1000) + \dot{r}(1000) \Delta t = R_T$$ $$6.4250 \times 10^6 - 1.3708 \times 10^3 \Delta t = 6378.14 \times 10^3 $$ à partir duquel: $$\Delta t= 34.184 \ s$$

La coordonnée $ \theta $ du site d'impact peut être estimée de manière similaire.

En utilisant à nouveau deux termes de la série Taylor, nous avons: $$\theta (1000 + \Delta t ) = \theta (1000) + \dot{\theta} (1000) \Delta t = 1.0083 + 1.1605 \times 10^{-3} \times (34.184) = 1.0480 \ rad = 60.00^\circ$$