Table des matières

Introduction
Idées de base de l'intégration numérique
      Exemple de calcul
La règle du trapèze composite
      La formule générale
      Implémentation
La méthode du point milieu composite
      L'idée
      La formule générale
      Implémentation
      Comparaison des méthodes du trapèze et du point milieu
Intégration Monte Carlo
      Exemple: détermination de \( \pi \)
      implémentation

Introduction

L'intégration numérique est un chapitre important de l'analyse numérique et un outil indispensable en physique numérique. On intègre numériquement dans deux cas principaux:

• on ne peut pas intégrer analytiquement,
• l'intégrande est fourni non pas sous la forme d'une fonction mais de tableaux de mesures, cas d'ailleurs le plus fréquent dans la vraie vie.

Les méthodes numériques d'intégration d'une fonction sont nombreuses et les techniques très diverses. Des très simples, comme la méthode des rectangles aux très complexes comme certaines variétés de la méthode de Monte-Carlo.

Idées de base de l'intégration numérique

Nous considérons l'intégrale $$ \begin{equation} \label{eq:ExempleIntegral} \int_a^b f(x)dx \end{equation} $$ La plupart des méthodes numériques de calcul de cette intégrale divisent l'intégrale d'origine en une somme de plusieurs intégrales, chacune couvrant une partie plus petite de l'intervalle d'intégration d'origine \( [a, b] \). Cette réécriture de l'intégrale est basée sur une sélection de points d'intégration \( x_i \), \( i = 0,1,…, n \) qui sont répartis sur l'intervalle \( [a, b] \). Les points d'intégration peuvent ou non être répartis uniformément. Une distribution uniforme simplifie les expressions et est souvent suffisante, nous nous limiterons donc principalement à ce choix. Les points d'intégration sont ensuite calculés comme: $$ \begin{equation} x_i = a + ih,\quad i = 0,1,\ldots,n \label{_auto1} \end{equation} $$ où $$ \begin{equation} h = \frac{b-a}{n} \label{_auto2} \end{equation} $$ Compte tenu des points d'intégration, l'intégrale d'origine est réécrite sous la forme d'une somme d'intégrales, chaque intégrale étant calculée sur le sous-intervalle entre deux points d'intégration consécutifs. L'intégrale dans \eqref{eq:ExempleIntegral} est donc exprimée comme: $$ \begin{equation} \label{eq:SumIntegrals} \int_a^b f(x)dx = \int_{x_0}^{x_1} f(x)dx + \int_{x_1}^{x_2} f(x)dx + \ldots + \int_{x_{n-1}}^{x_n} f(x)dx \end{equation} $$ Notez que \( x_0 = a \) et \( x_n = b \).

En partant de \eqref{eq:SumIntegrals}, les différentes méthodes d'intégration différeront dans la façon dont elles approchent chaque intégrale du côté droit. L'idée fondamentale est que chaque terme est une intégrale sur un petit intervalle \( [x_i, x_{i + 1}] \), et sur ce petit intervalle, il est logique d'approximer f par une forme simple, disons une constante, une ligne droite ou une parabole , que nous pouvons facilement intégrer à la main. Les détails deviendront clairs dans les exemples à venir.

Exemple de calcul

Pour comprendre et comparer les méthodes d'intégration numérique, il est avantageux d'utiliser une intégrale spécifique pour les calculs et les illustrations graphiques. En particulier, nous voulons utiliser une intégrale que nous pouvons calculer à la main de sorte que la précision des méthodes d'approximation puisse être facilement évaluée. Notre intégrale spécifique est tirée de la physique de base. Supposons que vous accélérez votre voiture du repos et demandez-vous jusqu'où vous allez en \( T \) secondes. La distance est donnée par l'intégrale \( \int_0^T v(t)dt \) , où \( v (t) \) est la vitesse en fonction du temps. Une fonction de vitesse en augmentation rapide pourrait être: $$ \begin{equation} v\left(t\right) = 3t^{2}e^{t^3}\thinspace \label{_auto3} \end{equation} $$ La distance après une seconde est $$ \begin{equation} \label{eq:SpeedIntegral} \int_0^1 v(t)dt \end{equation} $$ qui est l'intégrale que nous cherchons à calculer par des méthodes numériques. Heureusement, l'expression choisie de la vitesse a une forme qui permet de calculer facilement la primitive comme $$ \begin{equation} V(t) = e^{t^3}-1 \label{_auto4} \end{equation} $$ Nous pouvons donc calculer la valeur exacte de l'intégrale comme \( V (1) −V (0) ≈1.718 \) (arrondi à 3 décimales pour plus de commodité).

La règle du trapèze composite

L'intégrale \( \int_a^b f(x)dx \) peut être interprété comme l'aire entre l'axe des x et le graphique \( y = f (x) \) de fonction à intégrer. La figure 1 illustre cette zone de choix \eqref{eq:SpeedIntegral}. Le calcul de l'intégrale \( \int_0^1f(t)dt \) revient à calculer l'aire de la zone hachurée.

---

Figure 1: L'intégrale de \( v (t) \) interprétée comme l'aire sous le graphique de \( v \).

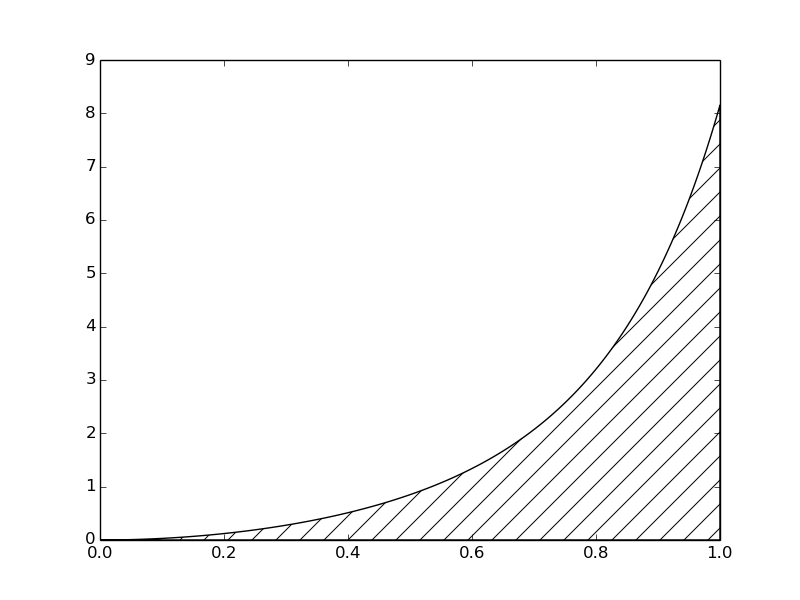
Si nous remplaçons le vrai graphique de la figure 1 par un ensemble de segments de ligne droite, nous pouvons voir la zone plutôt comme composée de trapèzes, dont les zones sont faciles à calculer. Ceci est illustré sur la figure 2, où 4 segments de ligne droite donnent naissance à 4 trapèzes, couvrant les intervalles de temps \( [0,0.2) \), \( [0.2,0.6) \), \( [0.6,0.8) \) et \( [0.8,1.0] \). Notez que nous en avons profité pour démontrer les calculs avec des intervalles de temps de tailles différentes.

---

Figure 2: Calculer approximativement l'intégrale d'une fonction comme la somme des aires des trapèzes.

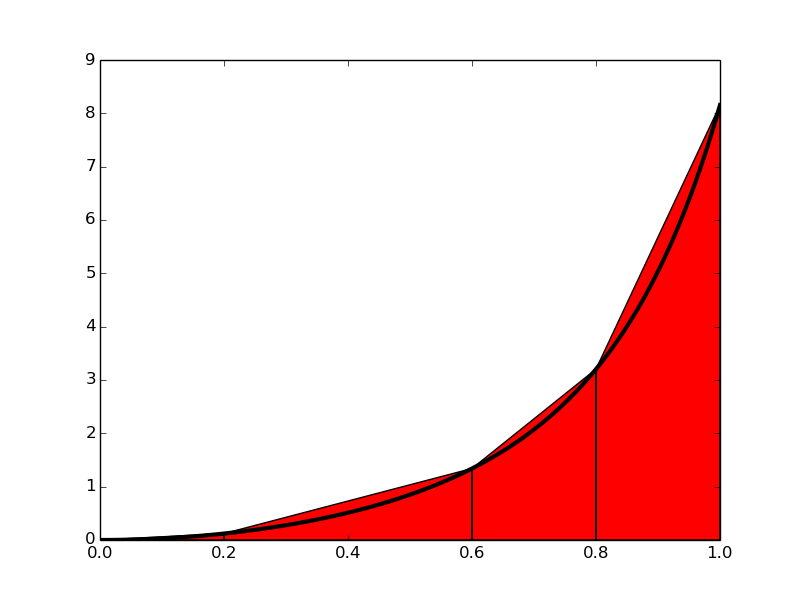
Les aires des 4 trapèzes représentés sur la figure 2 constituent maintenant notre approximation de l'intégrale \eqref{eq:SpeedIntegral}: $$ \begin{align} \int_0^1 v(t)dt &\approx h_1 (\frac{v(0)+v(0.2)}{2}) + h_2 (\frac{v(0.2)+v(0.6)}{2}) \nonumber \\ &+ h_3 (\frac{v(0.6)+v(0.8)}{2}) + h_4 (\frac{v(0.8)+v(1.0)}{2}) \label{eq:trapezoids} \end{align} $$ où $$ \begin{align} h_1 &= (0.2 - 0.0) \label{eq:h1}\\ h_2 &= (0.6 - 0.2) \label{eq:h2}\\ h_3 &= (0.8 - 0.6) \label{eq:h3}\\ h_4 &= (1.0 - 0.8) \label{eq:h4} \end{align} $$ Avec \( v(t) = 3t^{2}e^{t^3} \), chaque terme dans \eqref{eq:trapezoids} est facilement calculé et notre calcul approximatif donne $$ \begin{equation} \int_0^1 v(t)dt \approx 1.895 \label{_auto5} \end{equation} $$ Par rapport à la vraie réponse de \( 1.718 \), cela est d'environ \( 10 \% \). Cependant, notez que nous avons utilisé seulement 4 trapèzes pour approximer la zone. Avec plus de trapèzes, l'approximation serait devenue meilleure, puisque les segments de droite du côté supérieur des trapèzes suivraient alors le graphique de plus près. Faire un autre calcul avec plus de trapèzes n'est pas trop tentant pour un humain paresseux, mais c'est un travail parfait pour un ordinateur! Dérivons donc les expressions d'approximation de l'intégrale par un nombre arbitraire de trapèzes.

La formule générale

Pour une fonction donnée \( f (x) \), nous voulons approximer l'intégrale \( \int_a^bf(x)dx \) par \( n \) trapèzes (de largeur égale). Nous commençons par \eqref{eq:SumIntegrals} et approchons chaque intégrale du côté droit avec un seul trapèze. En détail, $$ \begin{align} \int_a^b f(x)\,dx &= \int_{x_0}^{x_1} f(x) dx + \int_{x_1}^{x_2} f(x) dx + \ldots + \int_{x_{n-1}}^{x_n} f(x) dx, \nonumber \\ &\approx h \frac{f(x_0) + f(x_1)}{2} + h \frac{f(x_1) + f(x_2)}{2} + \ldots + \nonumber \\ &\quad h \frac{f(x_{n-1}) + f(x_n)}{2} \label{eq:SumTrapezes} \end{align} $$ En simplifiant le côté droit de \eqref{eq:SumTrapezes}, nous obtenons $$ \begin{equation} \int_a^b f(x)\,dx \approx \\ \frac{h}{2}\left[f(x_0) + 2 f(x_1) + 2 f(x_2) + \ldots + 2 f(x_{n-1}) + f(x_n)\right] \label{_auto6} \end{equation} $$ qui est écrit de façon plus compacte comme $$ \begin{equation} \label{eq:GenralIntegral} \int_a^b f(x)\,dx \approx h \left[\frac{1}{2}f(x_0) + \sum_{i=1}^{n-1}f(x_i) + \frac{1}{2}f(x_n) \right] \end{equation} $$

Implémentation

Implémentation spécifique ou générale?

Supposons que notre objectif principal était de calculer l'intégrale spécifique \( \int_0^1 v(t)dt \) avec \( v(t)=3t^2e^{t^3} \). D'abord, nous avons joué avec un simple calcul de main pour voir de quoi il s'agissait, avant de développer (comme c'est souvent le cas en mathématiques) une formule générale \eqref{eq:GenralIntegral} pour l'intégrale générale ou «abstraite» \( \int_a^bf(x)dx \). Pour résoudre notre problème spécifique \( \int_0^1 v(t)dt \), nous devons ensuite appliquer la formule générale \eqref{eq:GenralIntegral} aux données données (fonction et limites intégrales) dans notre problème. Bien que simples en principe, les étapes pratiques sont déroutantes pour beaucoup car la notation dans le problème abstrait de \eqref{eq:GenralIntegral} diffère de la notation dans notre problème spécial. Clairement, les \( f \), \( x \) et \( h \) dans \eqref{eq:GenralIntegral} correspondent à \( v \), \( t \) et peut-être \( \Delta t \) pour la largeur du trapèze dans notre problème spécial.

La première alternative dans l'encadré ci-dessus semble moins abstraite et donc plus attrayante pour beaucoup. Néanmoins, comme nous l'espérons, cela sera évident à partir des exemples, la deuxième alternative est en fait la plus simple et la plus fiable d'un point de vue mathématique et de programmation. Ces auteurs affirmeront que la deuxième alternative est l'essence même du pouvoir des mathématiques, tandis que la première alternative est la source de beaucoup de confusion sur les mathématiques!

Implémentation avec fonctions

Pour l'intégrale \( \int_a^bf(x)dx \) calculée par la formule \eqref{eq:GenralIntegral}, nous voulons que le trapèze de la fonction Python correspondante prenne tout \( f \), \( a \), \( b \) et \( n \) en entrée et renvoie l'approximation à l'intégrale.

Nous écrivons une fonction Python trapeze() dans un fichier trapeze_integral.py aussi proche que possible de la formule \eqref{eq:GenralIntegral}, en nous assurant que les noms de variables correspondent à la notation mathématique:

Résoudre notre problème spécifique en une session

Le simple fait d'avoir la fonction trapeze() comme seul contenu d'un fichier trapeze_integral.py fait automatiquement de ce fichier un module que nous pouvons importer et tester dans une session interactive:

Calculons l'expression exacte et l'erreur dans l'approximation:

Cette erreur est-elle convaincante? On peut essayer un \( n \) plus grand:

Heureusement, beaucoup plus de trapèzes donnent une erreur beaucoup plus petite.

Résoudre notre problème spécifique dans un programme

Au lieu de calculer notre problème spécial dans une session interactive, nous pouvons le faire dans un programme. Comme toujours, un morceau de code faisant une chose particulière est mieux isolé en tant que fonction même si nous ne voyons aucune raison future d'appeler la fonction plusieurs fois et même si nous n'avons pas besoin d'arguments pour paramétrer ce qui se passe à l'intérieur de la fonction. Dans le cas présent, nous mettons simplement les instructions que nous aurions autrement mises dans un programme principal, à l'intérieur d'une fonction:

Maintenant, nous calculons notre problème spécial en appelant application() comme la seule instruction du programme principal.

Faire un module

Lorsque nous avons les différentes parties de notre programme comme une collection de fonctions, il est très simple de créer un module qui peut être importé dans d'autres programmes. Ce fait, avoir notre code comme module, signifie que la fonction trapeze() peut facilement être réutilisée par d'autres programmes pour résoudre d'autres problèmes. Les exigences d'un module sont simples: mettez tout à l'intérieur des fonctions et laissez les appels de fonction dans le programme principal être dans le soi-disant bloc de test:

Le test if est vrai si le fichier de module, trapeze_integral.py, est exécuté en tant que programme et faux si le module est importé dans un autre programme. Par conséquent, lorsque nous effectuons une importation: from trapeze_integral import trapeze dans un fichier, le test échoue et application() n'est pas appelée, c'est-à-dire que notre problème spécial n'est pas résolu et n'imprime rien à l'écran. D'un autre côté, si nous exécutons trapeze_integral.py dans la fenêtre du terminal, la condition de test est positive, application() est appelée et nous obtenons une sortie dans la fenêtre:

La méthode du point milieu composite

L'idée

Plutôt que d'approximer l'aire sous une courbe par des trapèzes, nous pouvons utiliser des rectangles simples. Il peut sembler moins précis d'utiliser des lignes horizontales et non des lignes obliques suivant la fonction à intégrer, mais une méthode d'intégration basée sur des rectangles (la méthode du point milieu) est en fait légèrement plus précise que celle basée sur des trapèzes!

Dans la méthode du milieu, nous construisons un rectangle pour chaque sous-intervalle où la hauteur est égale à \( f \) au milieu du sous-intervalle. Faisons-le pour quatre rectangles, en utilisant les mêmes sous-intervalles que nous avions pour les calculs manuels avec la méthode du trapèze: \( [0,0.2) \), \( [0.2,0.6) \), \( [0.6,0.8) \) et \( [0.8,1.0] \). On a $$ \begin{align} \int_0^1 f(t)dt &\approx h_1 f\left(\frac{0 + 0.2}{2}\right) + h_2 f\left(\frac{0.2 + 0.6}{2}\right) \nonumber \\ &+ h_3 f\left(\frac{0.6 + 0.8}{2}\right) + h_4 f\left(\frac{0.8 + 1.0}{2}\right) \label{_auto7} \end{align} $$ où \( h_1 \), \( h_2 \), \( h_3 \) et \( h_4 \) sont les largeurs des sous-intervalles, utilisées précédemment avec la méthode du trapèze et définies dans \eqref{eq:h1}-\eqref{eq:h4}.

---

Figure 3: Calcul approximatif de l'intégrale d'une fonction comme la somme des aires des rectangles.

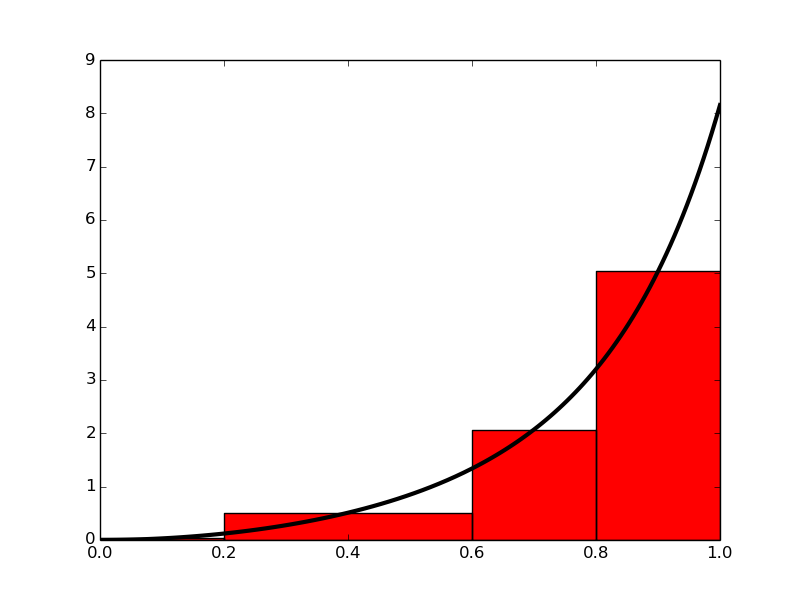
Avec \( f(t) = 3t^{2}e^{t^3} \), l'approximation devient \( 1.632 \). Comparé à la vraie réponse (\( 1.718 \)), c'est environ \( 5 \% \) trop petit, mais c'est mieux que ce que nous avons obtenu avec la méthode trapézoïdale (\( 10 \% \)) avec les mêmes sous-intervalles. Plus de rectangles donnent une meilleure approximation.

La formule générale

Dérivons une formule pour la méthode du milieu basée sur \( n \) rectangles d'égale largeur: $$ \begin{align} \int_a^b f(x)\,dx &= \int_{x_0}^{x_1} f(x)dx + \int_{x_1}^{x_2} f(x)dx + \ldots + \int_{x_{n-1}}^{x_n} f(x)dx, \nonumber \\ &\approx h f\left(\frac{x_0 + x_1}{2}\right) + h f\left(\frac{x_1 + x_2}{2}\right) + \ldots + h f\left(\frac{x_{n-1} + x_n}{2}\right) \label{_auto8}\\ &\approx h \left(f\left(\frac{x_0 + x_1}{2}\right) + f\left(\frac{x_1 + x_2}{2}\right) + \ldots + f\left(\frac{x_{n-1} + x_n}{2}\right)\right) \label{_auto9} \end{align} $$ Cette somme peut être écrite de façon plus compacte comme $$ \begin{equation} \label{eq:GeneralMidpoint} \int_a^b f(x) dx \approx h \sum_{i=0}^{n-1}f(x_i) \end{equation} $$ où \( x_i = \left(a + \frac{h}{2}\right) + ih \).

Implémentation

Nous suivons les conseils et les enseignements tirés de l'implémentation de la méthode trapèze et réalisons une fonction midpoint(f, a, b, n) (dans un fichier midpoint_integral.py) pour implémenter la formule générale \eqref{eq:GeneralMidpoint}:

Nous pouvons tester la fonction comme nous l'avons expliqué pour la méthode du trapèze similaire. L'erreur dans notre problème particulier \( \int_0^1 3t^2e^{t^3}dt \) avec quatre intervalles est maintenant d'environ \( 0.1 \) contrairement à \( 0.2 \) pour la règle du trapèze. Les différences sont rarement d'une importance pratique, et sur un ordinateur portable, nous pouvons facilement utiliser \( n = 10^6 \) et obtenir la réponse avec une erreur d'environ \( 10^{-12} \) en quelques secondes.

Comparaison des méthodes du trapèze et du point milieu

L'exemple suivant montre la facilité avec laquelle nous pouvons combiner les fonctions trapeze() et midpoint() pour comparer les deux méthodes dans le fichier compare_integration_methods.py:

Notez les efforts mis en forme agréable - la sortie devient

Une inspection visuelle des chiffres montre à quelle vitesse les chiffres se stabilisent dans les deux méthodes. Il semble que 13 chiffres se soient stabilisés dans les deux dernières lignes.

Intégration Monte Carlo

Les méthodes de Monte Carlo sont des techniques de calcul probabilistes. Au cœur, un algorithme de Monte Carlo représente de façon aléatoire certaines valeurs de l'espace de valeurs d'un paramètre considéré. La combinaison de plusieurs paramètres permet de tirer des conclusions stochastiques des relations. L'intégration des fonctions mathématiques de la forme: $$ \begin{equation*} A = \int_a^b f(x) \cdot dx \end{equation*} $$

Pour effectuer une intégration, nous voulons savoir comment les valeurs sélectionnées au hasard sont réparties: lesquelles des valeurs sont égales ou inférieures à la valeur de la fonction et lesquelles sont supérieures. Il s'agit d'une décision binaire qui divise les valeurs aléatoires en deux groupes. Du rapport de la taille des groupes, nous pouvons tirer nos conclusions.

Nous utilisons la fonction (intégrande) comme critère de décision uniquement. L'algorithme ne nous fournit rien d'autre que des comptes/fréquences. La fermeture probabiliste est alors: $$ \begin{equation*} \frac{\textrm{cas favorables}} {\textrm{cas possibles}} = \frac {n}{N} = \frac{A_{sous\;la\;fonction}}{A_{aire \;totale}} \end{equation*} $$ La zone \( A_{sous\;la\;fonction} \) est la zone inconnue qui nous intéresse. Pour \( A_{aire \;totale} \), nous choisissons arbitrairement une région simple, cette zone que nous pouvons calculer sans difficultés.

Exemple: détermination de \( \pi \)

À titre d'exemple, nous choisissons un cercle dont la fonction mathématique est donnée par la première: $$ \begin{align*} x^2 + y^2 &= R^2 \\ y = f(x) &= \sqrt{R^2 - x^2} \end{align*} $$ Pour l'estimation de \( \pi \), l'aire du cercle est comparée à l'aire du carré \( 2R \times 2R \), ce rapport est \( \pi / 4 \): $$ \begin{align*} A_{cercle} &= R^2 \cdot \pi \\ A_{carré} &= {(2R)}^2 = 4R^2 \end{align*} $$ Nous générons au hasard \( (x_rand, y_rand) \)-points. Pour chaque point, nous devons décider s'il se trouve à l'intérieur ou à l'extérieur du cercle. Pour cela, nous utilisons la différence \( y_{rand} - f(x_{rand}) \), où \( f(x) = \sqrt{R^2 - x^2} \) est la fonction d'un cercle dans le premier quadrant. Nous pouvons compter le nombre de points à l'intérieur du cercle. Nous pouvons compter le nombre de points à l'intérieur du cercle. Le rapport \( n / N \) est supposé être égal au rapport \( A_{cercle}/A_{carré} \) $$ \begin{align*} \frac {\textrm{n = (x,y)-points dans le cercle}} {\textrm{N = (x,y)-points dans le carré}} &= \frac{A_{cercle}}{A_{carré}} = \frac {R^2 \cdot \pi}{4R^2 } = \frac {\pi}{4} \\ \pi &= 4\frac{n}{N} \end{align*} $$

implémentation

Nous avons vu l'intégration de Monte Carlo lorsque nous avons calculé \( \pi / 4 \) en calculant l'aire du quart de cercle unitaire.

Voici le code:

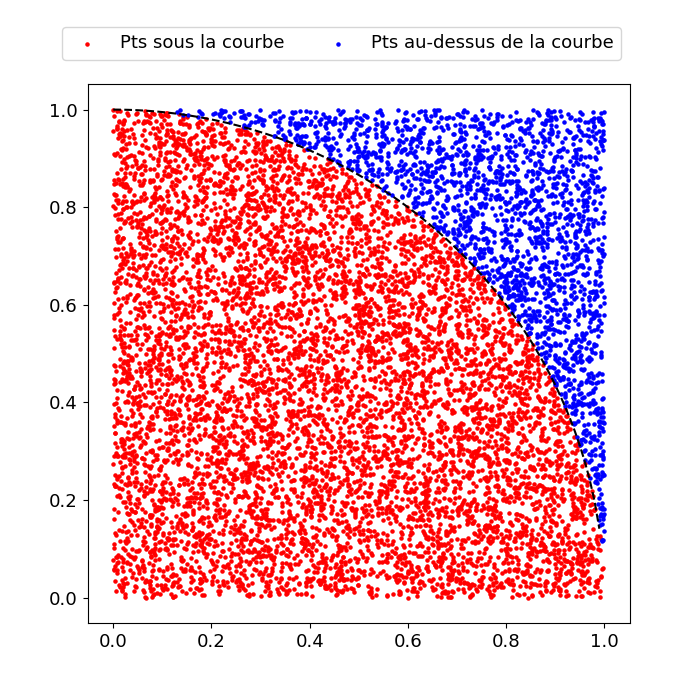
Nous pouvons généraliser cette approche aux courbes autres que \( y = \sqrt{1-x^2} \). L'idée est la suivante: pour une courbe arbitraire, trouvez le rectangle qui la contient, générez un point aléatoire dans ce rectangle et déterminez combien de points aléatoires se trouvent sous la courbe.