Résolution des équations aux dérivées partielles
Apr 15, 2020
Introduction
Il existe trois types d'équations aux dérivées partielles.- Des équations telles que l'équation d'onde,
où \( u (t, x) \) est une fonction de déplacement et \( c \) une vitesse constante, sont connues sous le nom d'équations hyperboliques.
- Des équations telles que l'équation de diffusion,
- Des équations telles que l'équation de Poisson,
On trouve des équations hyperboliques ou paraboliques dans les problèmes de valeurs initiales: la configuration du champ \( u (t, x) \) est spécifiée à un moment initial et évolue dans le temps. Les équations elliptiques se retrouvent dans les problèmes de valeur limite: la valeur du champ \( u (x, y, z) \) est spécifiée sur la limite d'une région et nous cherchons la solution à travers l'intérieur.
Équation de diffusion thermique
L'équation de diffusion thermique est historiquement liée à Joseph Fourier. Ce dernier naquit en 1768 à Auxerre, où il étudie dans une école militaire. Fin 1794, il est élève à Normale Sup et en 1795-1796, il enseigne la physique à Normale Sup et à l'X. Il débute ses travaux sur la chaleur en 1802 lorsqu'il est nommé préfet de l'Isère par Napoléon. Il publie sa théorie sur la chaleur (et l'analyse de Fourier) en 1822. Il est élu à l'Académie française en 1826 et décédé à Paris en 1830.
Figure 1: Gravure du mathématicien Jean Baptiste Joseph Fourier (1768-1830). (source 1: Article de CNRS Le journal, Joseph Fourier transforme toujours la science)

La conduction thermique dans les solides
Dans les solides, les molécules ou les atomes sont figés dans un réseau maillé qui empêchent les grands déplacements. Le seul mouvement possible est un mouvement de vibration autour de leur position d'équilibre dans le réseau. Le transfert thermique d'énergie se traduit par une augmentation plus ou moins grande de l'amplitude de ces vibrations. Lorsque l'énergie apportée est suffisante pour que l'amplitude de la vibration dépasse une certaine valeur dépendante du réseau, alors les molécules se libèrent du réseau et le solide fond et s'évapore...Le cas des métaux est un peu particulier : eux possèdent des électrons de conduction, qui circulent librement sur le réseau du solide. Ces électrons se comportent comme les molécules d'un gaz (on parle de gaz d'électrons) et dans ce cas, à l'augmentation de l'amplitude des vibrations sur le réseau s'ajoute le transfert d'énergie cinétique des électrons rapides, "chauds" vers les électrons lents, "froids".
Notion de flux d'énergie
La notion de flux d'énergie est très courante en physique. Nous l'avons déjà rencontré sous le nom d'intensité du courant électrique. Dans ce cas, il s'agit du flux de charges électriques qui traversent une surface unitaire donnée par unité de temps. Nous l'avons noté: $$ \begin{align} I_q = \dfrac{dQ}{dt} \label{_auto4} \end{align} $$ Par analogie, on définit le flux thermique, plus exactement le flux d'énergie interne par \( I_u = \dfrac{dU}{dt} \). C'est la quantité d'énergie interne U qui traverse, sans travail, une surface unitaire par unité de temps.Pour l'exprimer plus précisément, on introduit un nouvel objet par analogie avec le courant électrique. Il s'agit du vecteur de courant volumique d'énergie interne sans travail noté classiquement \( \vec{J_u} \) et souvent nommé improprement "vecteur courant thermique", ce qui nous permet d'écrire l'expression du flux de ce vecteur à travers une surface dS orientée vers l'extérieur par le vecteur normal \( \vec{n} \) , ce qui nous donne \( I_u = \int_S \vec{J_u} . \vec{n} dS \). Le signe de \( I_u \) dépend du sens du flux à travers la surface. Il est négatif pour le flux entrant et positif pour le flux sortant (pensez au signe du produit scalaire sous l'intégrale...).
L'expression de la loi de Fourier
Après ces préambules utiles, venons en à la loi de Fourier proprement dite. La conduction thermique est un transfert thermique spontané d'une région de température élevée vers une région de température plus basse, et est décrite par la loi dite de Fourier établie mathématiquement par Jean-Baptiste Biot en 1804 puis expérimentalement par Fourier en 1822 : la densité de flux de chaleur est proportionnelle au gradient de température.Pour faire simple, ici et dans la suite, on va se placer dans le cadre d'un problème unidimensionnel, c'est à dire que le transfert thermique d'énergie se fait sur une dimension \( Ox \).
La loi de Fourier relie, après constat expérimental, le vecteur de courant volumique d'énergie interne sans travail \( \vec{J_u} \) avec le gradient de température \( \vec{grad} T \). La relation est linéaire et s'écrit \( \vec{J_u} = - \kappa \ \vec{grad} T \). La linéarité de l'équation n'est due qu'aux approximations que nous avons fixé à son domaine de validité, comme pour la loi d'Ohm.
Le paramètre \( \kappa \) est appelé conductivité thermique, toujours positif, de dimension \( W.m^{-1}.K^{-1} \). Notez la présence du signe \( - \), qui résulte du second principe de la thermodynamique : le flux d'énergie va des régions aux températures les plus hautes vers les régions aux températures les plus basses.
Dans notre hypothèse d'un problème unidimensionnel, en développant le gradient, on obtient l'équation \( \vec{J_u} = - \kappa \dfrac{\partial T}{\partial x}\vec{u} \), soit en projetant sur \( Ox \), \( J_u(x,t) = - \kappa \dfrac{\partial T(x,t)}{\partial x} \) Nous obtenons une équation à deux variables, la position x et le temps t, avec une dérivée partielle.
Comment obtenir cette équation?
Nous allons l'établir en utilisant la loi de Fourier décrite ci-dessus et le principe de conservation d'énergie. Nous resterons dans le cadre du problème unidimensionnel, sachant que l'extension en dimension 2 ou 3 n'est pas très compliquée, mais trop lourde pour notre étude.Considérons un élément de volume dV orienté selon l'axe \( Ox \) de propagation du flux d'énergie, limité par deux surfaces dS, l'une entrante et l'autre sortante, et d'épaisseur \( dx \). Appelons \( \vec{J_uE} \) le vecteur de courant d'énergie volumique entrant et \( \vec{J_uS} \) le vecteur de courant d'énergie volumique sortant. Supposons que ces deux vecteurs soient normaux aux surfaces entrantes et sortantes.
Cet élément de volume \( dV \) est immobile et son énergie potentielle n'est pas modifiée par hypothèse. Selon le premier principe de la thermodynamique, la variation d'énergie interne dU n'est donc attribuable qu'à la variation \( dQ \), le transfert thermique d'énergie.
Calculons la variation d'énergie interne dans ce volume dV, de masse volumique \( \rho \), en utilisant la définition de \( \vec{J_u} \) donnée plus haut dans le cas unidimensionnel. Nous obtenons après simplification, en égalant \( dU \) et \( dQ \) : $$ \begin{align} \dfrac{\partial(\rho u)}{\partial t}dx = -J_{u,x}(x + dx,t) + J_{u,x}(x,t) \label{_auto5} \end{align} $$ En remarquant que \( J_{u,x}(x + dx,t) - J_{u,x}(x,t)= \dfrac{\partial J_{u,x}}{\partial x}dx \), on obtient finalement : $$ \begin{align} \dfrac{\partial(\rho u)}{\partial t} = - \dfrac{\partial J_{u,x}}{\partial x} \label{_auto6} \end{align} $$ Dans cette dernière équation, remplaçons dans le terme de droite \( J_{u,x} \) par sa définition donnée par la loi de Fourier, on obtient :
\( \dfrac{\partial(\rho u)}{\partial t} = - \dfrac{\partial}{\partial x}(- \kappa \dfrac{\partial T}{\partial x}) \) ou en condensant l'écriture : $$ \begin{align} \dfrac{\partial(\rho u)}{\partial t} = \kappa \dfrac{\partial^2 T}{\partial x^2} \label{_auto7} \end{align} $$ Vous aurez noté ici, si vous êtes attentifs, que j'ai considéré que \( \kappa \) était constant puisque je l'ai sorti de la dérivée sans autre forme de procès! C'est un peu osé, et vrai seulement si le milieu est isotrope (le matériaux est homogène) et si l'on ne chauffe pas trop fort ou trop vite, parce que sinon, il devient dépendant de la température.
Reste maintenant à traiter le terme de gauche. Pour ce faire, je vais faire appel à l'expression de la capacité calorique qui relie les variations de l'énergie avec les variations de température. On peut donc écrire que, si \( \rho u \) désigne l'énergie interne volumique : $$ \begin{align} \dfrac{\partial(\rho u)}{\partial t} = \rho c_v \dfrac{\partial T}{\partial t} \label{_auto8} \end{align} $$ avec \( c_v \) la capacité thermique massique à volume constant.
En reportant cette expression dans le terme de gauche de notre équation, j'obtiens : $$ \begin{align} \rho c_v \dfrac{\partial T}{\partial t} = \kappa \dfrac{\partial^2 T}{\partial x^2} \label{_auto9} \end{align} $$ soit en regroupant les termes constants à droite de l'équation : $$ \begin{align} \dfrac{\partial T}{\partial t} = \dfrac{\kappa}{\rho c_v} \dfrac{\partial^2 T}{\partial x^2} \label{_auto10} \end{align} $$ Pour simplifier l'écriture, je vais appeler \( D \) le rapport \( \dfrac{\kappa}{\rho c_v} \). Ce paramètre est la diffusivité thermique du matériau constituant notre élément de volume. La dimension de \( D \) est \( m^2.s^{-1} \). Finalement, j'obtiens l'équation : $$ \begin{align} \label{eq:diffT} \dfrac{\partial T}{\partial t} = D \dfrac{\partial^2 T}{\partial x^2} \end{align} $$ qui constitue l'équation de diffusion thermique!
Résolution numérique de l'équation de diffusion thermique
Le modèle physique
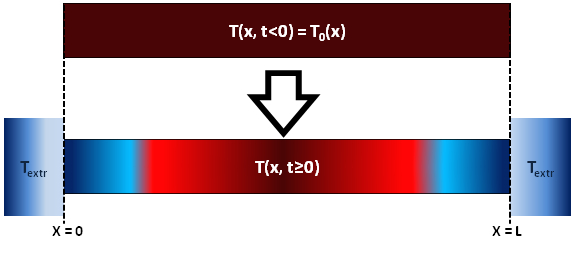
Nous allons considérer une barre métallique homogène de faible diamètre, de telle sorte que nous puissions négliger ses dimensions spatiales autre que sa longueur. Autrement dit, je m'arrange pour avoir un modèle approximativement 1D.Nous allons considérer que cette barre solide de longueur \( L = 1m \) de coefficient de diffusion thermique \( D \approx 0.5 \ m^2.s^{-1} \). La barre est initialement préparée dans un état de température \( T(x, t < 0) = T_0(x) = 100 C^\circ \).
À l'instant \( t \ge 0 \), les extrémités de la barre spnt misent en contact avec deux sources de températures identiques \( T_{extr} = 0 c^\circ \), donc nous aurons: $$ \begin{align*} T(x = 0, t \ge 0) = T(x = L, t \ge 0) = T_{extr} \end{align*} $$
Figure 2: Choc thermique sur une barre de longueur L.
La température \( T(x, t) \) de la barre est solution de l'équation \eqref{eq:diffT} de la diffusion thermique à 1D
Principe de la résolution numérique
On recherche une solution numérique à ce problème par la classique méthode des différences finies.Supposons que nous cherchions l'évolution de \( T(x,t) \) sur une durée totale \( \tau = 1 s \):
- La barre est spatialement discrétisée en \( N_x \) tronçons de longueur égale \( \Delta x = \dfrac{L}{N_x} \). Ainsi, l'abscisse discrète \( x_m \) est: \( x_m = m * \Delta x \) avec \( m \in [0, N_x] \).
- De même, la durée totale de l'évolution est discrétisée en \( N_t \) intervalles de durée \( \Delta t = \dfrac{\tau}{N_t} \). Ainsi, l'instant "discret" \( t_n \) est: \( t_n = n * \Delta t \) avec \( n \in [0, N_t] \).
Discrétisation du terme \( \dfrac{\partial T}{\partial t} \)
Pour \( x \) fixe (\( x=x_m \)), \( T(x_m, t) \) est de classe \( C^1 \) sur \( [0, \tau] \) par rapport au temps.
Soit le développement de Taylor à l'ordre 1: $$ \begin{align*} T(x_m, t_{n+1}) &= T(x_m, t_n+ \Delta t) \\ &\approx T(x_m, t_n) + \Delta t \dfrac{\partial T(x_m, t_n)}{\partial t} + \mathcal{O}(\Delta t^2) \end{align*} $$ Nous revenons à l'expression explicite d'Euler déjà abordée dans le chapitre précédent. On peut donc avoir l'expression discrétisée du terme \( \dfrac{\partial T}{\partial t} \): $$ \begin{align} \label{eq:terme1} \dfrac{\partial T(x_m, t_n)}{\partial t} &= \dfrac{T(x_m, t_{n+1}) - T(x_m, t_n)}{\Delta t} \end{align} $$
Discrétisation du terme \( \dfrac{\partial^2 T}{\partial x^2} \)
Pour \( t \) fixe (\( t=t_n \)), \( T(x, t_n) \) est de classe \( C^2 \) sur \( [0, L] \) par rapport à \( x \).
Soit le développement de Taylor à l'ordre 2: $$ \begin{align*} T(x_{m+1}, t_n) &= T(x_m + \Delta x, t_n) \\ &\approx T(x_m, t_n) + \Delta x \dfrac{\partial T(x_m, t_n)}{\partial x} + \dfrac{\Delta x^2}{2!} \dfrac{\partial^2 T(x_m, t_n)}{\partial x^2} + \mathcal{O}(\Delta t^3) \end{align*} $$
La dérivée première \( \dfrac{\partial T(x_m, t_n)}{\partial x} \) ne figure pas dans l'équation initiale (Eq. \eqref{eq:diffT}), il faut donc l'éliminer!
Note
L'idée est de faire une addition des développements en (\( x_m + \Delta x \)) et en (\( x_m - \Delta x \)).
Remplaçons les équations \eqref{eq:terme1} et \eqref{eq:terme2} dans l'équation \eqref{eq:diffT} de la diffusion thermique. Ainsi l'équation de la diffusion thermique 1D discrétisée s'écrit: $$ \begin{align} \dfrac{T(x_m, t_{n+1}) - T(x_m, t_n)}{\Delta t} \approx D \dfrac{T(x_{m+1}, t_n) - 2 T(x_m, t_n) + T(x_{m-1}, t_n)}{\Delta x^2} \label{_auto11} \end{align} $$ D'où l'on tire finalement la relation de récurrence permettant d'obtenir la température en \( x_m \) à l'instant \( t_{n+1} \) en fonction des températures \( T_{m,n} \), \( T_{m+1,n} \) et \( T_{m-1,n} \) calculées à l'instant \( t_n \): $$ \begin{align} \label{eq:diffTFinal} T(x_m, t_{n+1}) \approx T(x_m, t_n) + D \dfrac{\Delta t}{\Delta x^2} \left[T(x_{m+1}, t_n) - 2 T(x_m, t_n) + T(x_{m-1}, t_n) \right] \end{align} $$
Note
On peut écrire l'expression \eqref{eq:diffTFinal} avec la notation suivante: $$ \begin{align*} T_{m,n+1} \approx T_{m,n} + D \dfrac{\Delta t}{\Delta x^2} \left[T_{m+1,n} - 2 T_{m,n} + T_{m-1,n} \right] \end{align*} $$
Code Python
Le programme Python pour ce problème est:
Nous pouvons modifier le code ci-dessus pour créer une animation de l'évolution du système dans le temps:
## NOM DU PROGRAMME: EDP_DiffChalAnim.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
# DONNÉES NUMÉRIQUES
L = 1 # Longueur de la barre [m]
Nx = 100 # Nombre de tronçons
tau = 1 # Durée totale de l'évolution [s]
Nt = 10000 # Nombre d'intervalles de temps
dx = L/Nx # Longueur du tronçon
dt = tau/Nt # Intervalle élémentaire de temps
D = 0.5 # Coefficient de diffusion thermique
Tb = 100 # Température initiale de la barre
Textr = 0 # Température des extrémités
# Construction de axe des abscisses (variable espace x)
x = np.linspace(0, L, Nx)
# Construction CI ,CL (2 exemples pour la CI)
T = [Textr] + (Nx - 2)*[Tb] + [Textr] # Echelon de temperature
#T=Textr + (Tb-Textr ) * np.sin(np.pi*x/L) # Arche sinusoidale temperature
# Construction du tableau vierge des accroissements de temperature
accroissT = np.zeros(Nx)
T[0] = 0
# Corps de la résolution
for n in range(Nt): # Boucle d'évolution de temps pas à pas
plt.clf()
for m in range(1, Nx-1): #boucle de calcul de accroissement de temperature pour chaque abscisse
accroissT[m] = ((dt*D)/(dx**2))*(T[m-1]-2*T[m]+T[m+1])
for m in range(1, Nx-1): # Boucle de calcul de T instant suivant
T[m] += accroissT[m]
if (n%100 == 0):
plt.figure(1)
plotlabel ="t=%1.2f s"%(n*dt)
plt.plot(x, T, lw = 4, label=plotlabel, color = plt.get_cmap('jet')(1-n/Nt))
plt.grid()
plt.xlabel("x [m]", fontsize=14)
plt.ylabel("T [C]", fontsize=14)
plt.title("Évolution de la température après le choc thermique", weight ="bold")
plt.legend(loc=1)
plt.axis([0,L,0,100])
plt.tight_layout()
plt.show()
plt.pause(0.001)
Lors de l'exécution de ce code, nous aurons l'animation ci-dessous:
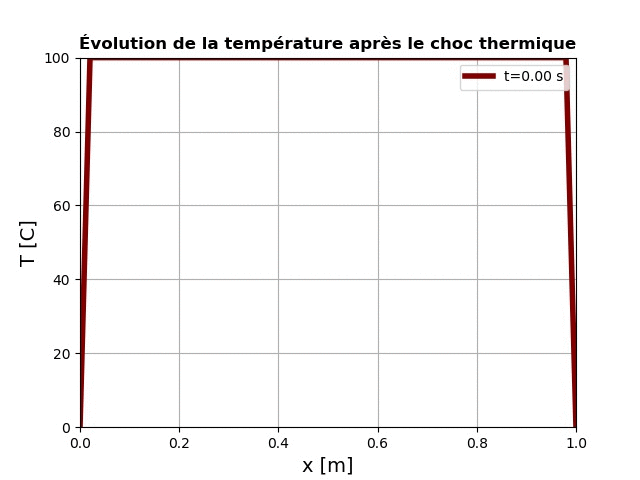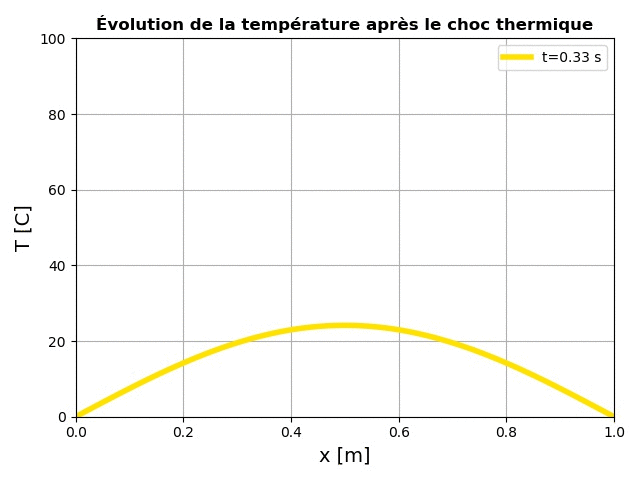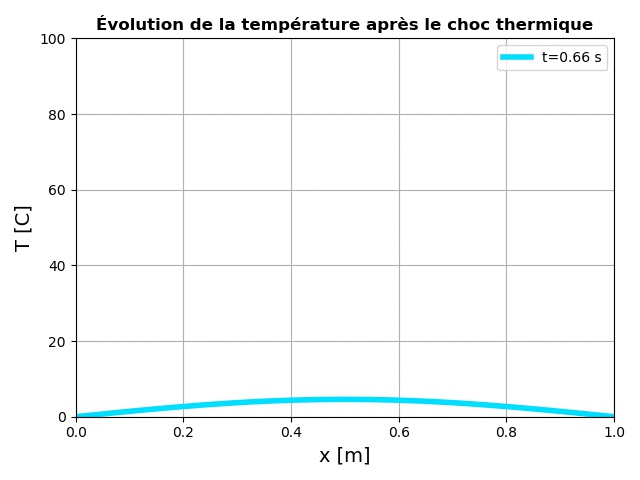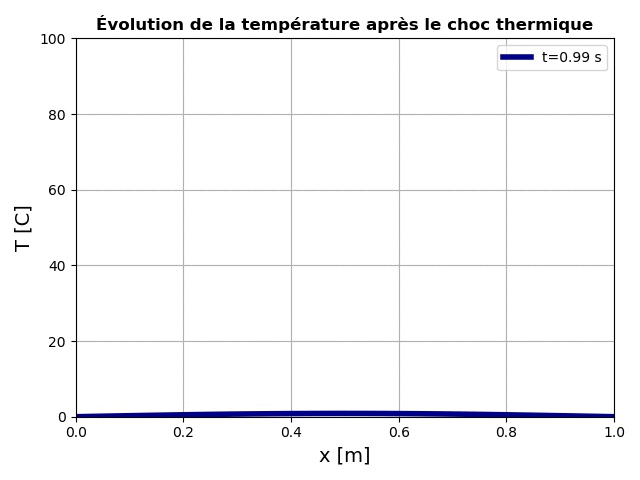
L'équation de Schrödinger "time-dependent"
Soit une particule, un électron pour fixer les idées, qui se déplace dans un espace unidimensionnel. Pour étudier son mouvement, nous allons fixer un référentiel. L'apparition de ce mot "référentiel" devrait vous interpeller : la relativité n'est pas loin ! On ne va pas se compliquer la vie et on considérera que la vitesse de la particule est petite devant c, un électron non relativiste. Pour rappel, si la particule est relativiste, ne surtout pas utiliser Schrödinger...
Cet électron bouge dans un espace où il peut subir des interactions avec d'autres systèmes physiques. Dans ce cas, on modélisera ces interactions par une énergie potentielle notée U(x,t). Si l'électron ne subit aucune interaction, U(x,t) sera nulle et notre électron sera dit "libre".
L'équation, analogue à notre deuxième loi de Newton, qui décrit le mouvement de l'électron dans l'espace et le temps est l'équation de Schrödinger. Plus précisément, elle décrit l'évolution de la fonction d'onde qui elle-même décrit l'état quantique de l'électron. Sa forme unidimensionnelle s'écrit : $$ \begin{align} i\hbar \dfrac{\partial \Psi (x,t)}{\partial t} = -\dfrac{\hbar ^2}{2m_e} \dfrac{\partial^2 \Psi (x,t)}{\partial x^2} + U(x)\Psi(x,t) \label{_auto12} \end{align} $$ avec \( m_e \) la masse de l'électron et \( \hbar \) la constante de Planck réduite. Je choisis d'utiliser une fonction potentiel U stationnaire (indépendante du temps).
Figure 3: Erwin Schrödinger (1887-1961).Physicien théoricien de nationalité autrichienne. Il a reçu un prix Nobel de physique 1933 partagé avec Paul Adrien Maurice Dirac "pour la découverte de nouvelles formes productives de la théorie atomique."

C'est une équation linéaire de premier ordre par rapport au temps. Linéaire, c'est à dire que toute combinaison linéaire de solutions particulières de l'équation est aussi solution de l'équation. De premier ordre par rapport au temps, c'est à dire que la connaissance de l'état quantique de la particule à un instant donné, considéré comme l'instant initial \( t_0 \), permet de calculer son état quantique à n'importe quel instant postérieur à \( t_0 \).
L'énoncé du problème
On enferme un électron dans une boite quantique, c'est à dire qu'on se cantonne dans un espace fermé par des barrières de potentiel infini. Nous resterons dans un espace unidimensionnel, ce qui nous donne le schéma suivant de boîte :
Figure 4: Le potentiel est nul dans la boîte et infini ailleurs.

Dans cette boîte, nous déposons un électron et nous voulons déterminer son mouvement. Pour l'instant, notre électron ne rencontre aucune barrière de potentiel dans sa boîte. Il est libre... dans sa boîte ! La fonction U(x) est donc constante et nulle dans la boîte.
La simulation de l'évolution d'un électron libre U(x) = 0
L'équation de Schrödinger 1D avec U(x) = 0, que l'on écrit \( i\hbar \dfrac{\partial \Psi (x,t)}{\partial t} = -\dfrac{\hbar ^2}{2m} \dfrac{\partial^2 \Psi (x,t)}{\partial x^2} \) st parfaitement intégrable analytiquement! D'ailleurs, je vous invite à la comparer avec une autre équation que nous avons déjà rencontré: \( \dfrac{\partial T}{\partial t} = D \dfrac{\partial^2 T}{\partial x^2} \), l'équation de diffusion thermique! Dans les deux cas, la transformée de Fourier est l'outil privilégié pour ces calculs.
La discrétisation de Schrödinger
La première étape consiste à discrétiser l'équation de Schrödinger. Reprenons donc notre équation de Schrödinger time-dependent dans un espace unidimensionnel : $$ \begin{align} i\hbar \dfrac{\partial \Psi (x,t)}{\partial t} = -\dfrac{\hbar ^2}{2m} \dfrac{\partial^2 \Psi (x,t)}{\partial x^2} + U(x)\Psi(x,t) \label{_auto13} \end{align} $$ La fonction \( \Psi(x,t) \) est une fonction complexe. Je vais la décomposer en sa partie réelle \( \Psi_R(x,t) \) et sa partie imaginaire \( \Psi_I(x,t) \) et écrire deux équations l'une portant sur sa partie réelle et l'autre sur sa partie imaginaire, ce qui, en réorganisant notre équation de Schrödinger pour isoler à gauche la dérivée partielle temporelle, nous donne le couple d'équations : $$ \begin{align} \dfrac{\partial \Psi_R (x,t)}{\partial t} &= -\dfrac{\hbar}{2m} \dfrac{\partial^2 \Psi_I (x,t)}{\partial x^2} + \dfrac{1}{\hbar}U(x)\Psi_I(x,t) \label{_auto14}\\ \dfrac{\partial \Psi_I (x,t)}{\partial t} &= \dfrac{\hbar}{2m} \dfrac{\partial^2 \Psi_R (x,t)}{\partial x^2} - \dfrac{1}{\hbar}U(x)\Psi_R(x,t) \label{_auto15} \end{align} $$Comme d'habitude je vais discrétiser les dérivées partielles en faisant un DL d'ordre 1 : $$ \begin{align} \dfrac{\partial \Psi(x,t)}{\partial t} &\approx \dfrac{\Psi(x, t+\Delta t) - \Psi(x,t)}{\Delta t} \label{_auto16}\\ \dfrac{\partial^2 \Psi(x,t)}{\partial x^2} &\approx \dfrac{\Psi(x+\Delta x,t) - 2\Psi(x,t) + \Psi(x - \Delta x,t)}{{\Delta x}^2} \label{_auto17} \end{align} $$
Nous obtenons finalement les équations discrètes, avec \( i \) l'indice sur le vecteur \( x \) : $$ \begin{align} \Psi_R(i) &= \Psi_R(i) - \dfrac{\hbar \Delta t }{2m{\Delta x}^2}\left( \Psi_I(i+1) - 2\Psi_I(i) + \Psi_I(i-1) \right) + \dfrac{e \Delta t}{\hbar} U(i) \Psi_I(i) \label{_auto18}\\ \Psi_I(i) &= \Psi_I(i) + \dfrac{\hbar \Delta t }{2m{\Delta x}^2}\left( \Psi_R(i+1) - 2\Psi_R(i) + \Psi_R(i-1) \right) - \dfrac{e \Delta t}{\hbar} U(i) \Psi_R(i) \label{_auto19} \end{align} $$
Une petite remarque : j'ai introduit la charge élémentaire e dans la valeur du coefficient affectant l'énergie potentielle U : c'est parce que j'exprime dans mon code U en eV, il faut donc effectuer la conversion eV/Joule.
Dans mon code, j'ai défini \( a_2 = \dfrac{\hbar \Delta t}{2m{\Delta x}^2} = 0.1 \), il faut bien faire un choix, ce qui me donne la contrainte sur \( \Delta t \) suivante, codée dans la variable dt : dt = a2*2*m_e*dx**2/hbar.
Le code Python
La propagation du paquet d'ondes
Le programme Python pour ce problème est:
## NOM DU PROGRAMME: Schrodinger_1DLibre.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
'''
Définition des constantes
-------------------------
Les constantes physiques standards sont tirées
du package scipy.constants
'''
from scipy.constants import h, hbar, e, m_e
DeuxPi = 2.0*np.pi
L = 5.0e-9 # dimension de la boite quantique (USI)
#%% Définition du domaine spatial et temporel
Nx = 1000 # nombre de pas d'intégration sur le domaine spatial
xmin = 0.0
xmax = L
dx = (xmax-xmin)/Nx
x = np.arange(0.0,L,dx)
Nt = 30000 # nombre de pas d'intégration sur le domaine temporel
a2 = 0.1
dt = a2*2*m_e*dx**2/hbar
a3 = e*dt/hbar
#%% Définition des paramètres du paquet d'onde inital
x0 = x[int(Nx/2)] # position initiale du paquet
sigma = 2.0e-10 # largeur du paquet en m
Lambda = 1.5e-10 # longeur d'onde de de Broglie l'électron (en m)
Ec = (h/Lambda)**2/(2*m_e*e) # énergie cinétique théorique de l'électron (en eV)
#%% Définition du potentiel
U = np.zeros(Nx) # électron libre dans le puit
#%% Initialisation des buffers de calcul aux conditions initiales
Psi_Real = np.zeros(Nx)
Psi_Imag = np.zeros(Nx)
Psi_Prob = np.zeros(Nx)
#%% calcul et affichage de la fonction d'onde initiale
Psi_Real = np.exp(-0.5*((x-x0)/sigma)**2)*np.cos(DeuxPi*(x-x0)/Lambda)
Psi_Imag = np.exp(-0.5*((x-x0)/sigma)**2)*np.sin(DeuxPi*(x-x0)/Lambda)
# Normalisation du paquet d'onde
Psi_Prob = Psi_Real**2 + Psi_Imag**2
## FIGURE ---> Test
#plt.figure()
#pl1, pl2, pl3 = plt.plot(x, Psi_Real, x, Psi_Imag, x, Psi_Prob)
#plt.legend((pl1, pl2,pl3), ("PSI R", "PSI Imag", "Psi Prob"))
#plt.show()
#%% Boucle de calcul et d'affichage de l'évolution
for t in range(Nt):
plt.clf()
Psi_Real[1:-1] = Psi_Real[1:-1] - a2*(Psi_Imag[2:] - 2*Psi_Imag[1:-1] + Psi_Imag[:-2]) \
+ a3*U[1:-1]*Psi_Imag[1:-1]
Psi_Imag[1:-1] = Psi_Imag[1:-1] + a2*(Psi_Real[2:] - 2*Psi_Real[1:-1] + Psi_Real[:-2]) \
- a3*U[1:-1]*Psi_Real[1:-1]
Psi_Prob[1:-1] = Psi_Real[1:-1]**2 + Psi_Imag[1:-1]**2
if t % 1000 == 0:
plt.figure(1)
plt.plot(x*1.e9,Psi_Real,'blue')
plt.plot(x*1.e9,Psi_Imag,'red')
plt.plot(x*1.e9,Psi_Prob,'green')
plt.axis([0,L*1.e9,-1,1])
plt.grid(True)
plt.tight_layout()
plt.savefig("anim2/"+str(int(t%Nt/1000)).rjust(2, '0')+".png")
plt.savefig("anim2/myimage.pdf")
plt.show()
plt.pause(0.001)
Lors de l'exécution de ce code, nous aurons l'animation ci-dessous:
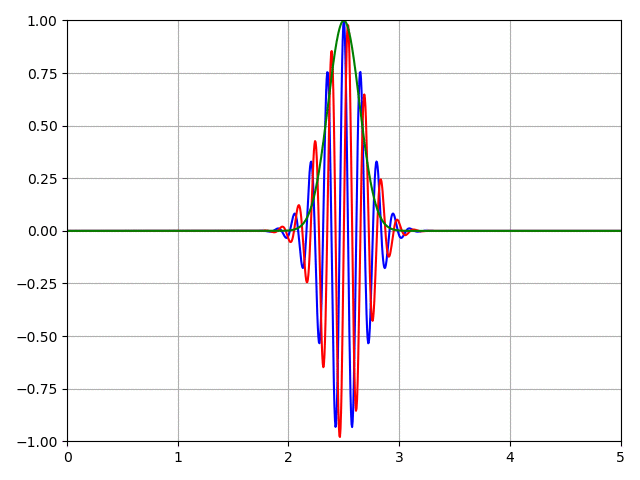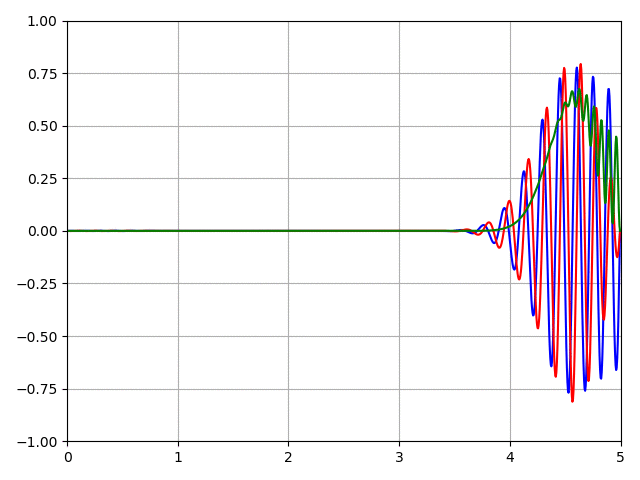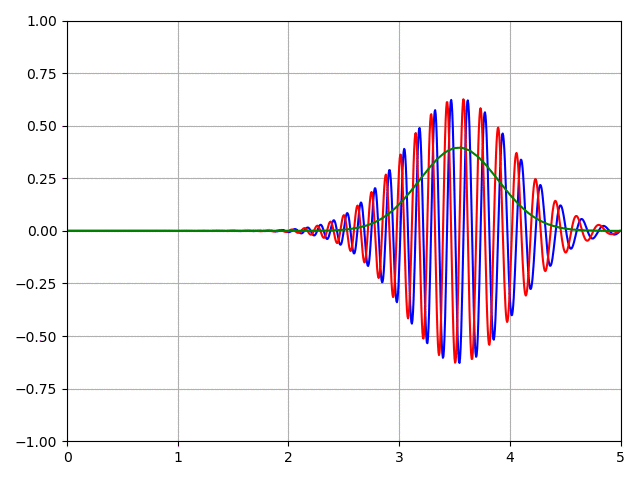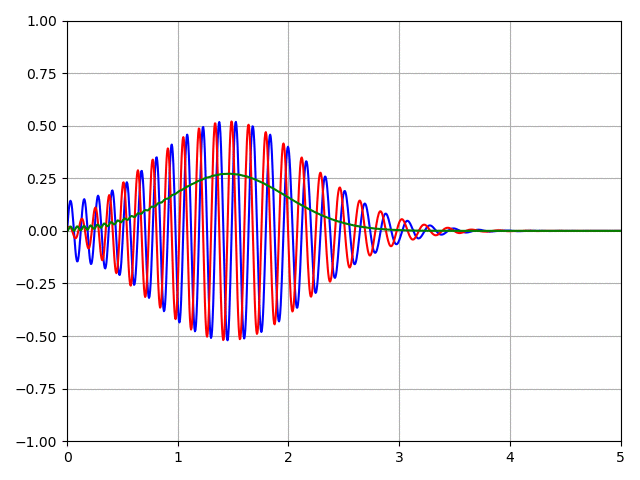
Cas d'une barrière de potentiel Le programme Python pour ce problème est:
## NOM DU PROGRAMME: Schrodinger_1DBar.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
'''
Définition des constantes
-------------------------
Les constantes physiques standards sont tirées
du package scipy.constants
'''
from scipy.constants import h, hbar, e, m_e
DeuxPi = 2.0*np.pi
L = 5.0e-9 # dimension de la boite quantique (USI)
#%% Définition du domaine spatial et temporel
Nx = 1000 # nombre de pas d'intégration sur le domaine spatial
xmin = 0.0
xmax = L
dx = (xmax-xmin)/Nx
x = np.arange(0.0,L,dx)
Nt = 50000 # nombre de pas d'intégration sur le domaine temporel
a2 = 0.1
dt = a2*2*m_e*dx**2/hbar
a3 = e*dt/hbar
#%% Définition des paramètres du paquet d'onde inital
x0 = x[int(Nx/4)] # position initiale du paquet
sigma = 2.0e-10 # largeur du paquet en m
Lambda = 1.5e-10 # longeur d'onde de de Broglie l'électron (en m)
Ec = (h/Lambda)**2/(2*m_e*e) # énergie cinétique théorique de l'électron (en eV)
#%% Définition du potentiel
U0 = 80 # en eV
U = np.zeros(Nx)
#U[int(Nx/2):] = U0 # définition d'une marche de potentiel
EppBar = 30 # largeur de la barrière en nombre de pas dx (0.15 nm)
U[int(Nx/2):int(Nx/2+EppBar)] = U0 # définition d'une barrière de potentiel
#%% Initialisation des buffers de calcul aux conditions initiales
Psi_Real = np.zeros(Nx)
Psi_Imag = np.zeros(Nx)
Psi_Prob = np.zeros(Nx)
#%% calcul et affichage de la fonction d'onde initiale
Psi_Real = np.exp(-0.5*((x-x0)/sigma)**2)*np.cos(DeuxPi*(x-x0)/Lambda)
Psi_Imag = np.exp(-0.5*((x-x0)/sigma)**2)*np.sin(DeuxPi*(x-x0)/Lambda)
# Normalisation du paquet d'onde
Psi_Prob = Psi_Real**2 + Psi_Imag**2
## FIGURE ---> Test
#plt.figure()
#pl1, pl2, pl3 = plt.plot(x, Psi_Real, x, Psi_Imag, x, Psi_Prob)
#plt.legend((pl1, pl2,pl3), ("PSI R", "PSI Imag", "Psi Prob"))
#plt.show()
#%% Boucle de calcul et d'affichage de l'évolution
for t in range(Nt):
plt.clf()
Psi_Real[1:-1] = Psi_Real[1:-1] - a2*(Psi_Imag[2:] - 2*Psi_Imag[1:-1] + Psi_Imag[:-2]) \
+ a3*U[1:-1]*Psi_Imag[1:-1]
Psi_Imag[1:-1] = Psi_Imag[1:-1] + a2*(Psi_Real[2:] - 2*Psi_Real[1:-1] + Psi_Real[:-2]) \
- a3*U[1:-1]*Psi_Real[1:-1]
Psi_Prob[1:-1] = Psi_Real[1:-1]**2 + Psi_Imag[1:-1]**2
if t % 1000 == 0:
fig, ax1 = plt.subplots(num=1)
ax1.plot(x*1.e9,Psi_Prob,'green')
ax1.axis([0,L*1.e9,0,1])
ax1.set_xlabel('x [nanometre]')
ax1.set_ylabel('Densite de proba. de detection [m-1]')
ax1.grid(True)
ax2 = ax1.twinx()
ax2.plot(x*1.e9,U,'blue')
ax2.set_ylabel('U [eV]')
ax2.axis([0,L*1.e9,0,90])
plt.savefig("anim3/"+str(int(t%Nt/1000)).rjust(2, '0')+".png")
plt.savefig("anim3/myimage.pdf")
plt.tight_layout()
plt.show()
plt.pause(0.001)
Lors de l'exécution de ce code, nous aurons l'animation ci-dessous:
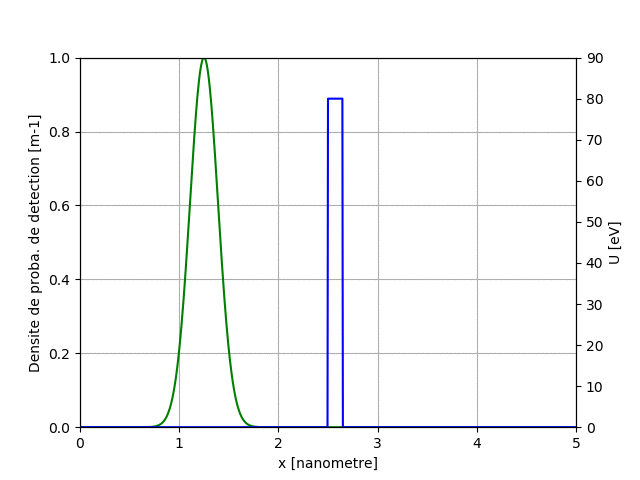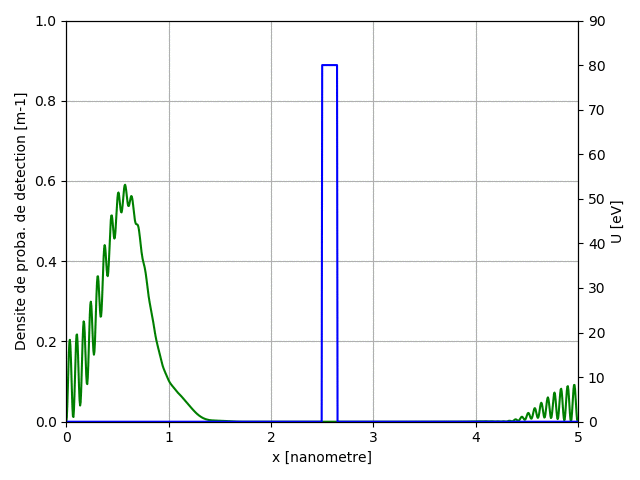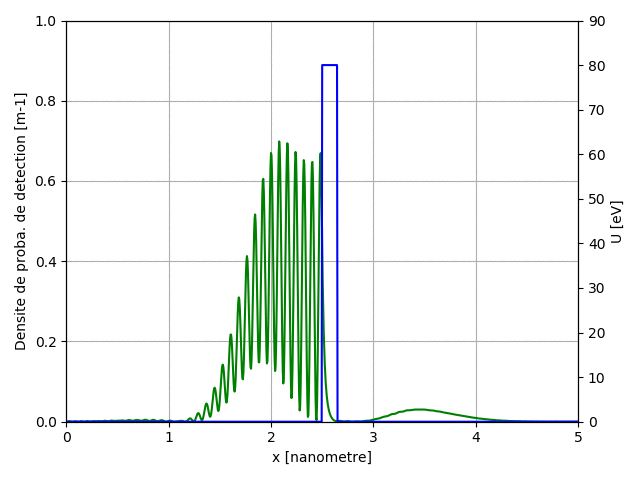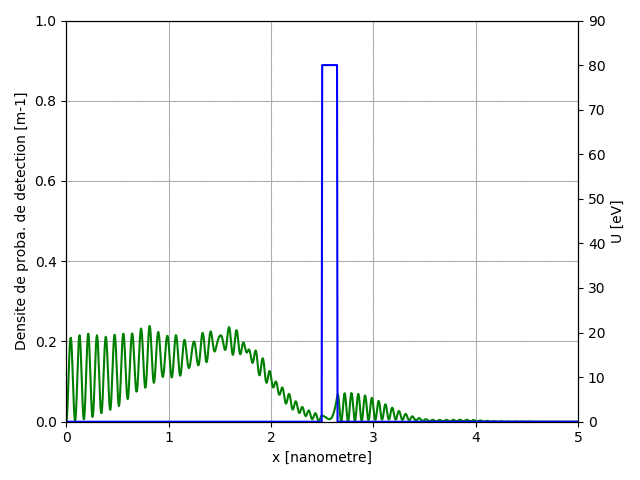
L'équation de Laplace
Nous considérons maintenant les équations elliptiques. L'équation de Poisson en trois dimensions est : $$ \begin{align} \dfrac{\partial^2 u(x, y, z)}{\partial x^2} + \dfrac{\partial^2 u(x, y, z)}{\partial y^2} + \dfrac{\partial^2 u(x, y, z)}{\partial z^2} &= - \dfrac{\rho(x,y,z)}{\epsilon_0} \label{_auto20} \end{align} $$ où \( u(x, y, z) \) est le champ de potentiel électrique et \( \rho(x, y, z) \) est la densité de charge. Par souci de simplicité, cependant, nous étudierons l'équation de Laplace en deux dimensions : $$ \begin{align} \dfrac{\partial^2 u(x, y)}{\partial x^2} + \dfrac{\partial^2 u(x, y)}{\partial y^2} &= 0 \label{_auto21} \end{align} $$ sur le carré \( 0 ≤ x ≤ L \) et \( 0 ≤ y ≤ L \) avec une paroi du carré maintenue (la paroi à \( y = L \)) à un potentiel de \( V_0 = 1V \) et les autres parois mises à la terre à \( 0V \).
Figure 5: Exemple de problème de valeur limite pour l'équation de Laplace en deux dimensions.
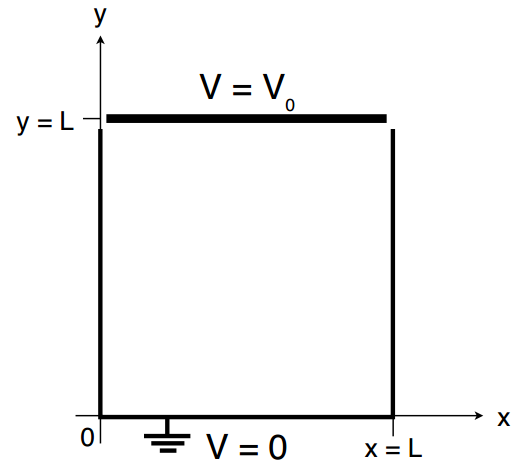
Nous utilisons la séparation des variables $$ \begin{align} u(x, y) &= X(x)Y(y) \label{_auto22} \end{align} $$ pour exprimer l'équation de Laplace comme les équations différentielles ordinaires $$ \begin{align} - \dfrac{X"}{X} &= \dfrac{Y"}{Y} = k^2 \label{_auto23} \end{align} $$ où \( k \) est une constante de séparation. Les conditions aux limites sont \( X (0) = 0 \), \( X (L) = 0 \), \( Y (0) = 0 \) et \( Y (L) = V_0 \). Les solutions pour \( X \) avec ces conditions aux limites sont $$ \begin{align} X(x) \propto sin(\dfrac{n \pi x}{L}) \quad pour \ n = 1,2,3,\dots \label{_auto24} \end{align} $$ et les constantes de séparation autorisées sont \( k_n = n \pi /L \). Les solutions pour \( Y \) seront une combinaison linéaire des fonctions sinus hyperbolique et cosinus hyperbolique, mais comme seule la fonction sinus hyperbolique disparaît à \( x = 0 \), notre solution est de la forme $$ \begin{align} u(x,y) = \sum_{n=1}^{\infty} c_n sin(\dfrac{n \pi x}{L}) sinh(\dfrac{n \pi y}{L}) \label{_auto25} \end{align} $$ La condition aux limites finale, \( u (x, L) = V_0 \), détermine alors les coefficients \( c_n \) : on a $$ \begin{align} \sum_{n=1}^{\infty} c_n sinh(n \pi) sin(\dfrac{n \pi x}{L}) &=V_0 \label{_auto26} \end{align} $$ Nous multiplions les deux côtés par \( sin (m \pi x = L) \) et intégrons de \( x = 0 \) à \( x = L \) pour obtenir $$ \begin{equation} \dfrac{L}{2} sinh(m \pi) = \begin{cases} \dfrac{2LV_0}{m \pi} & \text{pour m impair}\\ 0 & \text{autrement.} \end{cases} \label{_auto27} \end{equation} $$ Nous avons donc $$ \begin{equation} c_m = \begin{cases} \dfrac{4V_0}{m \pi \ sinh(m \pi)} & \text{pour m impair}\\ 0 & \text{autrement.} \end{cases} \label{_auto28} \end{equation} $$ et la solution de l'équation de Laplace est $$ \begin{equation} u(x,y) = 4 V_0 \sum_{\substack{n=1 \\ n \ impair}}^{\infty} \dfrac{sin(n \pi x/L)}{n \pi} \dfrac{sinh(n \pi y/L)}{sinh(n \pi)} \label{_auto29} \end{equation} $$ Un grand nombre de termes dans cette série sont nécessaires pour calculer avec précision le champ près du mur près de \( y = L \) (et surtout aux coins).
La méthode de relaxation peut être utilisée pour les équations elliptiques de la forme $$ \begin{equation} \hat{L} u = \rho \label{_auto30} \end{equation} $$ où \( \hat{L} \) est un opérateur elliptique et \( \rho \) est un terme source. L'approche consiste à prendre une distribution initiale \( u \) qui ne résout pas nécessairement l'équation elliptique et à lui permettre de se détendre à la solution de l'équation en faisant évoluer l'équation de diffusion $$ \begin{equation} \dfrac{\partial u}{\partial t}= \hat{L} u - \rho \label{_auto31} \end{equation} $$ Aux temps tardifs, \( t \rightarrow 0 \), la solution s'approchera asymptotiquement de la solution stationnaire de l'équation elliptique. Pour le problème en question (\( \rho = 0 \) et \( \hat{L} \) est l'opérateur laplacien bidimensionnel), la méthode FTCS appliquée à l'équation de diffusion conduit à $$ \begin{equation} u_{j,k}^{n+1} = u_{j,k}^{n} + \left[ \dfrac{u_{j+1,k}^{n} - 2 u_{j,k}^{n} + u_{j-1,k}^{n}}{(\Delta x)^2} + \dfrac{u_{j,k+1}^{n} - 2 u_{j,k}^{n} + u_{j,k-1}^{n}}{(\Delta y)^2}\right] \Delta t \label{_auto32} \end{equation} $$ où \( u_{j,k}^{n} = u^{n}(j \Delta x, k \Delta y) \) et \( n \) indique l'itération. Pour simplifier, nous prenons \( \Delta x = \Delta y = \Delta \) donc nous avons $$ \begin{equation} u_{j,k}^{n+1} = (1 - \omega) u_{j,k}^{n} + \dfrac{\omega}{4}(u_{j+1,k}^{n} + u_{j-1,k}^{n} + u_{j,k+1}^{n} + u_{j,k-1}^{n}) \label{eq:laplaceFTCS} \end{equation} $$ où \( \omega = 4 \Delta t /\Delta^2 \). La stabilité de l'équation de diffusion limite l'ampleur des \( \omega \). Nous pouvons déterminer la valeur maximale de \( \omega \) en utilisant une analyse de stabilité de von Neumann, mais maintenant nous nous limiterons aux modes propres spatiaux qui satisfont aux conditions aux limites de Dirichlet pour la partie homogène de la solution. Notre approche est donc $$ \begin{equation} u_{j,k}^{n} = u^0 \zeta^n(m_x, m_y) sin(\dfrac{m_x \pi j \Delta}{L}) sin(\dfrac{m_y \pi k \Delta}{L}) \label{eq:approche} \end{equation} $$ où \( m_x \) et \( m_y \) sont respectivement les numéros de mode dans les directions \( x \) et \( y \). En substituant cette approche à l'Eq. \eqref{eq:laplaceFTCS} on trouve $$ \begin{equation} \zeta(m_x, m_y) = 1 - \omega + \dfrac{\omega}{2} \left( cos(\dfrac{m_x \pi \Delta}{L}) + cos(\dfrac{m_y \pi \Delta}{L}) \right) \label{eq:zeta} \end{equation} $$ et nous voyons que la stabilité est atteinte, c'est-à-dire que \( | \zeta(m_x, m_y) | \le 1 \) pour tout mode donné par \( (m_x, m_y) \), si \( \omega \le 1 \). Si nous prenons maintenant la plus grande valeur de \( \Delta t = \Delta^2 / 4 \) permise pour une itération stable correspondant à \( \omega = 1 \), nous obtenons l'itération suivante schème: $$ \begin{equation} u_{j,k}^{n+1} = \dfrac{1}{4} (u_{j+1,k}^{n}+u_{j-1,k}^{n}+u_{j,k+1}^{n}+u_{j,k-1}^{n}) \label{_auto33} \end{equation} $$ On voit ici que la valeur du champ à un point de réseau donné \( (j, k) \) à l'étape \( n + 1 \) est égale à la moyenne des valeurs du champ aux points voisins à l'étape \( n \). Ceci est connu comme la méthode de Jacobi.
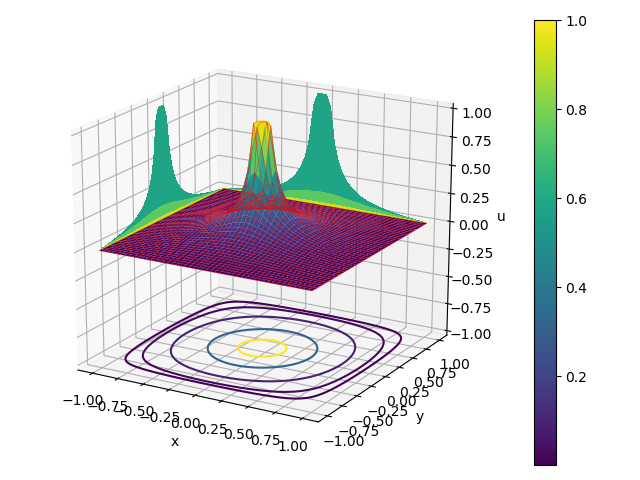
Le programme Laplace_relax.py implémente la méthode de Jacobi pour notre problème de modèle. Le nombre de points de grille de chaque côté, \( N \), est entré. Les résultats obtenus pour \( N = 20 \) points sont présentés sur la figure 6.
## NOM DU PROGRAMME: Laplace_relax.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
eps = 1e-5 # erreur fractionnaire autorisée
L = 1.0 # longueur de chaque côté
N = int(input('nombre de points de grille sur un côté -> '))
dy = dx = L/(N-1.0)
x = np.array(range(N))*dx
y = np.array(range(N))*dy
(x, y) = np.meshgrid(x, y)
u0 = np.zeros((N, N))
u1 = np.zeros((N, N))
# conditions aux limites
for j in range(N):
u1[j,N-1] = u0[j,N-1] = 1.0
# préparer l'animation
image = plt.imshow(u0.T, origin='lower', extent=(0.0, L, 0.0, L))
n = 0 # nombre d'itérations
err = 1.0 # erreur moyenne par site
while err > eps:
# mettre à jour le tracé animé
image.set_data(u0.T)
plt.title('itération %d'%n)
plt.tight_layout()
plt.show()
plt.pause(0.001)
# prochaine itération en raffinement
n = n+1
err = 0.0
for j in range(1, N-1):
for k in range(1, N-1):
u1[j,k] = (u0[j-1,k]+u0[j+1,k]+u0[j,k-1]+u0[j,k+1])/4.0
err += abs(u1[j,k]-u0[j,k])
err /= N**2
# permutez les anciens et les nouveaux tableaux pour la prochaine itération
(u0, u1) = (u1, u0)
# tracé de surface de la solution finale
fig = plt.figure()
axis = fig.gca(projection='3d', azim=-60, elev=20)
surf = axis.plot_surface(x, y, u0.T, rstride=1, cstride=1, cmap='viridis')
wire = axis.plot_wireframe(x, y, u0.T, rstride=1+N//50, cstride=1+N//50,
color = "r", linewidth=0.5, alpha = 0.5)
axis.contour(x, y, u0.T, 10, zdir='z', offset=-1.0)
axis.set_xlabel('x')
axis.set_ylabel('y')
axis.set_zlabel('u')
axis.set_zlim(-1.0, 1.0)
fig.colorbar(surf)
plt.tight_layout()
plt.savefig("Laplace_relax.png"); plt.savefig("Laplace_relax.pdf")
plt.show()
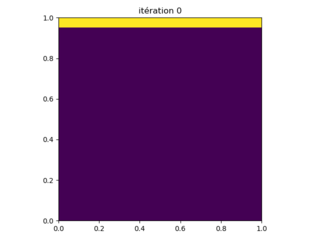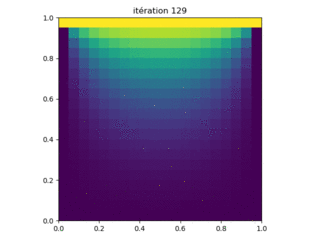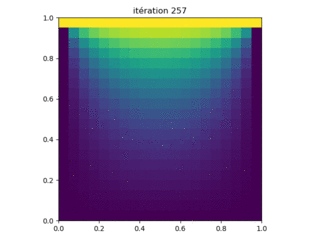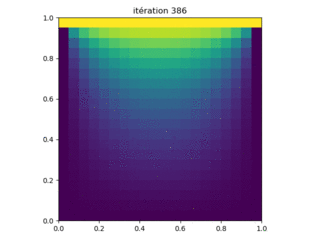
Figure 6: Résultats de l'exécution du programme Laplace_relax.py avec les paramètres N = 20 points de grille de chaque côté. La solution est obtenue après 386 itérations.
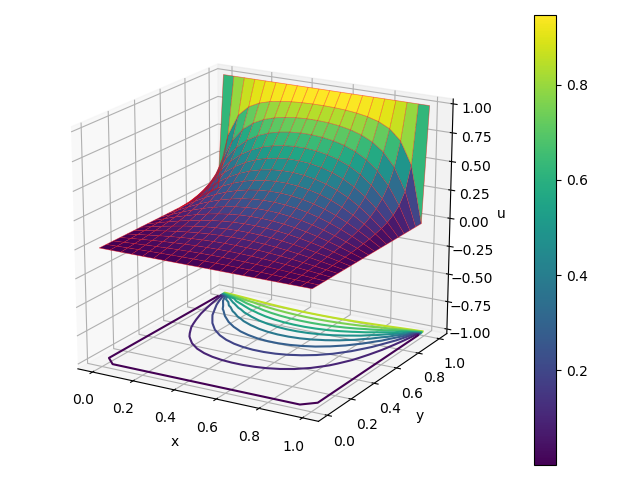
Dans le programme Laplace_relax.py, l'itération s'est poursuivie jusqu'à ce que l'erreur moyenne par point de maillage soit inférieure à \( \epsilon = 10^{-5} \) où l'erreur a été estimée en prenant la différence entre l'ancienne valeur à l'étape \( n \) et la nouvelle valeur à l'étape \( n + 1 \). Le nombre d'itérations nécessaires à la convergence dépend du mode propre en décomposition le plus lent de l'itération. Le module du mode de décomposition le plus lent est connu sous le nom de rayon spectral
$$
\begin{equation}
\rho = max_{m_x, m_y} |\zeta(m_x, m_y)|.
\label{_auto34}
\end{equation}
$$
De l'Eq. \eqref{eq:zeta} nous voyons que pour la méthode de Jacobi avec \( \omega = 1 \) nous avons
$$
\begin{equation}
\rho = \rho_J = cos(\dfrac{\pi \Delta}{L}).
\label{_auto35}
\end{equation}
$$
ce qui correspond au mode \( m_x = m_y = 1 \). Chaque itération multiplie l'erreur résiduelle dans ce mode le moins amorti par un facteur de module \( \rho \) et donc le nombre d'itérations nécessaires pour atteindre la tolérance d'erreur souhaitée \( \epsilon \) sera
$$
\begin{equation}
n = \dfrac{ln \epsilon}{ln \rho}.
\label{_auto36}
\end{equation}
$$
Pour la méthode Jacobi, \( \rho_J = 1 - \dfrac{1}{2} (\pi/N) \) et ainsi
$$
\begin{equation}
n \approx \dfrac{2 |ln \epsilon|}{\pi^2} N^2.
\label{_auto37}
\end{equation}
$$
Notez que si nous doublons le nombre de points de grille \( N \), nous avons besoin de quatre fois plus d'itérations pour converger. Pour les problèmes pratiques, la méthode de Jacobi converge trop lentement pour être utile.
Pour progresser, considérons à nouveau l'Eq. \eqref{eq:laplaceFTCS} et notons que si nous imaginons que notre grille de calcul est divisée en points clairs et sombres décalés, comme le montre la figure 7, puis pour mettre à jour la valeur d'un point blanc, nous n'avons besoin que de la valeur actuelle à ce point blanc et des valeurs des points sombres voisins et vice versa pour mettre à jour la valeur d'un point sombre.
Figure 7: Un réseau décalé de points sombres et clairs pour une utilisation en sur-relaxation successive. Les points gris font partie de la frontière et ne sont pas évolués. Pour mettre à jour un point blanc ne nécessite que la valeur précédente du point blanc et des points sombres environnants et de même pour mettre à jour un point noir ne nécessite que la valeur précédente des points noirs et des points clairs environnants.
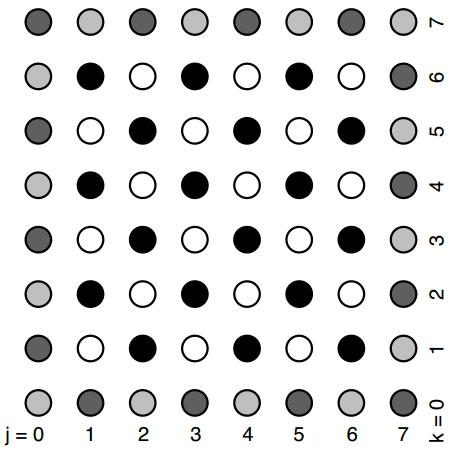
Ainsi, nous pouvons adopter une approche échelonnée où nous mettons à jour tous les points blancs, puis nous mettons à jour tous les points noirs et les deux étapes peuvent être effectuées sur place. Pour les étapes où \( n \) est un entier, nous calculons les valeurs des points blancs en utilisant la formule $$ \begin{equation} u_{j,k}^{n+1} = (1 - \omega) u_{j,k}^{n} + \dfrac{\omega}{4}(u_{j+1,k}^{n+1/2} + u_{j-1,k}^{n+1/2} + u_{j,k+1}^{n+1/2} + u_{j,k-1}^{n+1/2}) \label{eq:surrelax2D} \end{equation} $$ puis pour les étapes où n est un demi-entier, nous utilisons la même formule pour calculer les valeurs des points noirs. Nous pouvons répéter l'analyse de stabilité en utilisant l'approche de l'équation. \eqref{eq:approche} et nous trouvons $$ \begin{equation} \zeta^{1/2}(m_x, m_y) = \dfrac{\omega c \pm \sqrt{\omega^2 c^2 - 4(\omega -1)}}{2} \label{_auto38} \end{equation} $$ où $$ \begin{equation} c =\dfrac{1}{2} (cos(\dfrac{m_x \pi \Delta}{L}) + cos(\dfrac{m_y \pi \Delta}{L})) \label{_auto39} \end{equation} $$ Cela révèle que le schéma de l'Eq. \eqref{eq:surrelax2D} est stable pour \( 0 < \omega < 2 \). Lorsque \( \omega = 1 \), la méthode est connue sous le nom de méthode Gauss-Seidel, qui converge un peu plus rapidement que la méthode Jacobi. Pour \( \omega> 1 \), nous avons accéléré la convergence (par rapport à la relaxation) qui est connue sous le nom de sur-relaxation successive ou SOR (Successive Over-Relaxation, en anglais). Le paramètre \( \omega \) est connu comme le paramètre de sur-relaxation.
Il existe une valeur optimale pour le paramètre de sur-relaxation pour lequel le rayon spectral est minimisé. Si nous nous concentrons sur le mode le moins amorti pour lequel \( m_x = m_y = 1 \), nous avons \( c = \rho_J \) et donc le rayon spectral en fonction de \( \omega \) peut être écrit comme $$ \begin{equation} \rho(\omega) = \begin{cases} \left[ \dfrac{1}{2} \omega \rho_J + \dfrac{1}{2} \sqrt{\omega^2 \rho_J^2 - 4(\omega - 1)} \right]^2 & \quad pour \ 0 < \omega \le \omega_{opt}\\ \omega -1 & \quad pour \ \omega_{opt} \le \omega < 2 \end{cases} \label{_auto40} \end{equation} $$ où \( \omega_{opt} \) est le choix optimal qui minimise \( \rho \), $$ \begin{equation} \omega_{opt} = \dfrac{2}{1 + \sqrt{1 - \rho_J^2}} = \dfrac{2}{1 + sin(\pi \Delta/L)} \quad pour \ \rho_J = cos(\pi \Delta/L). \label{_auto41} \end{equation} $$ Ainsi, ou le choix optimal du paramètre de sur-relaxation, \( \omega = \omega_{opt} \approx \pi = N \), le rayon spectral est $$ \begin{equation} \rho(\omega_{opt})= \rho_{opt} = \dfrac{1 - sin(\pi \Delta/L)}{1 + sin(\pi \Delta/L)} \approx 1 - \dfrac{2\pi}{N} \label{_auto42} \end{equation} $$ et le nombre d'itérations nécessaires pour réduire l'erreur à une certaine tolérance \( \epsilon \) est $$ \begin{equation} n \approx \dfrac{ln \epsilon}{ln \rho_{opt}} \approx \dfrac{|ln \epsilon|}{2 \pi} N. \label{_auto43} \end{equation} $$ Maintenant, le nombre d'itérations est proportionnel à \( N \) plutôt qu'à \( N^2 \), donc la convergence est atteinte beaucoup plus rapidement pour les grandes valeurs de \( N \).
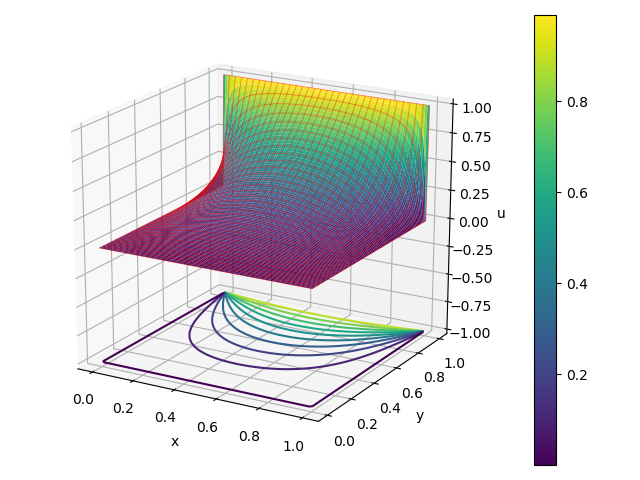
Le programme Laplace_surrelax.py est une modification de Laplace_relax.py qui implémente une sur-relaxation successive. Le programme diffère dans de nombreux endroits, il est donc répertorié dans son intégralité. Les résultats pour \( N = 100 \) points le long d'un côté sont affichés sur la figure 8. La convergence se produit en 137 itérations.
## NOM DU PROGRAMME: Laplace_surrelax.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
eps = 1e-5 # erreur fractionnaire autorisée
L = 1.0 # longueur de chaque côté
N = int(input('nombre de points de grille sur un côté -> '))
dy = dx = L/(N-1.0)
x = np.array(range(N))*dx
y = np.array(range(N))*dy
(x, y) = np.meshgrid(x, y)
u = np.zeros((N, N))
# conditions aux limites
for j in range(N):
u[j,N-1] = 1.0
# calculer le paramètre de sur-relaxation
omega = 2.0/(1.0+np.sin(np.pi*dx/L))
# pixels blancs et noirs: les blancs ont j+k pairs; les noirs ont j+k impairs
blanc = [(j, k) for j in range(1, N-1) for k in range(1, N-1) if (j+k)%2 == 0]
noir = [(j, k) for j in range(1, N-1) for k in range(1, N-1) if (j+k)%2 == 1]
# préparer l'animation
image = plt.imshow(u.T, origin='lower', extent=(0.0, L, 0.0, L))
n = 0 # nombre d'itérations
err = 1.0 # erreur moyenne par site
while err > eps:
# mettre à jour le tracé animé
image.set_data(u.T)
plt.title('itération %d'%n)
plt.tight_layout()
plt.show()
plt.pause(0.001)
# prochaine itération en raffinement
n = n+1
err = 0.0
for (j, k) in blanc+noir: # boucle sur pixels blancs puis pixels noirs
du = (u[j-1,k]+u[j+1,k]+u[j,k-1]+u[j,k+1])/4.0-u[j,k]
u[j,k] += omega*du
err += abs(du)
err /= N**2
# tracé de surface de la solution finale
fig = plt.figure()
axis = fig.gca(projection='3d', azim=-60, elev=20)
surf = axis.plot_surface(x, y, u.T, rstride=1, cstride=1, cmap='viridis')
wire = axis.plot_wireframe(x, y, u.T, rstride=1+N//50, cstride=1+N//50,
color = "r", linewidth=0.5, alpha = 0.5)
axis.contour(x, y, u.T, 10, zdir='z', offset=-1.0)
axis.set_xlabel('x')
axis.set_ylabel('y')
axis.set_zlabel('u')
axis.set_zlim(-1.0, 1.0)
fig.colorbar(surf)
plt.tight_layout()
plt.savefig("Laplace_surrelax.png"); plt.savefig("Laplace_surrelax.pdf")
plt.show()
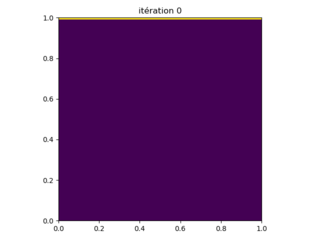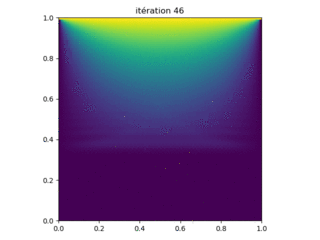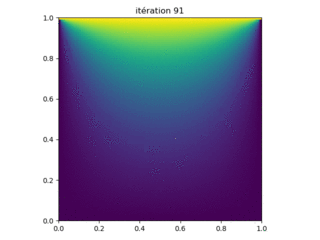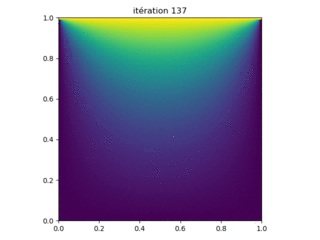
Figure 8: Résultats de l'exécution du programme LaplaceJacobi_surrelax.py avec les paramètres N = 100 points de grille le long de chaque côté. La solution est obtenue après 137 itérations.
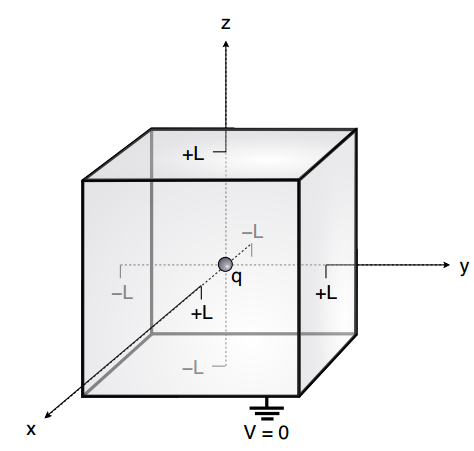
Comme dernier exemple, résolvons le potentiel électrique produit par une charge ponctuelle centrée dans un cube avec des bords de longueur \( 2L \) dans laquelle les faces du cube sont mises à la terre comme le montre la figure 9.
Figure 9: Exemple de problème de valeur limite pour l'équation de Poisson : une charge ponctuelle \( q \) est située au centre d'un cube de longueur d'arête \( 2L \) dont les faces sont mises à la terre.
Il s'agit maintenant d'un problème tridimensionnel que nous pouvons à nouveau résoudre en utilisant une sur-relaxation successive, et notre équation d'itération comprend désormais également un terme source: $$ \begin{equation} u_{i,j,k}^{n+1} = (1 - \omega) u_{i,j,k}^{n} + \dfrac{\omega}{6}(u_{i+1,j,k}^{n+1/2} + u_{i-1,j,k}^{n+1/2} + u_{i,j+1,k}^{n+1/2} + u_{i,j-1,k}^{n+1/2} + u_{i,j,k+1}^{n+1/2} + u_{i,j,k-1}^{n+1/2}) + \dfrac{\omega}{6} \dfrac{\rho_{i,j,k}}{\epsilon_0} \label{eq:surrelax3D} \end{equation} $$ Encore une fois, nous divisons le réseau de points de la grille en pixels «blancs» et «noirs» alternés et résolvons les pixels blancs sur les pas entiers et les pixels noirs sur les pas demi-entiers. La charge ponctuelle nous donne une densité de charge que nous considérons comme étant $$ \begin{equation} \rho_{i,j,k} = \begin{cases} \dfrac{q}{\Delta^3} & \quad pour \ i = j = k = (N-1)/2\\ 0 & \text{autrement} \end{cases} \label{_auto44} \end{equation} $$ et nous devons être sûrs de choisir une valeur impaire pour \( N \) afin qu'il y ait un point de grille au centre exact de la boîte.
Le programme charge.py répertorié ci-dessous calcule le champ de potentiel électrique dans la boîte mise à la terre pour une unité \( q = \epsilon_0 = 1 \) charge. Les résultats sont présentés sur la figure 10.
## NOM DU PROGRAMME: charge.py
#% IMPORTATION
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
eps = 1e-5 # erreur fractionnaire autorisée
L = 1.0 # longueur de chaque côté
N = int(input('nombre de points de grille sur un côté -> '))
dz = dy = dx = 2.0*L/(N-1.0)
x = -L + np.array(range(N))*dx
y = -L + np.array(range(N))*dy
z = -L + np.array(range(N))*dz
u = np.zeros((N, N, N))
rho = np.zeros((N, N, N))
# source
q = 1.0
rho[(N-1)//2,(N-1)//2,(N-1)//2] = q/(dx*dy*dz)
# préparer l'animation
s = u[:,:,(N-1)//2]
image = plt.imshow(s.T, origin='lower', extent=(-L, L, -L, L), vmax=1.0)
# calculer le paramètre de sur-relaxation
omega = 2.0/(1.0+np.sin(np.pi*dx/L))
# pixels blancs et noirs: les blancs ont i+j+k pairs; les noirs ont i+j+k impairs
blanc = [(i, j, k) for i in range(1, N-1) for j in range(1, N-1) \
for k in range(1, N-1) if (i+j+k)%2 == 0]
noir = [(i, j, k) for i in range(1, N-1) for j in range(1, N-1) \
for k in range(1, N-1) if (i+j+k)%2 == 1]
n = 0 # nombre d'itérations
err = 1.0 # erreur moyenne par site
while err > eps:
image.set_data(s.T)
plt.title('itération %d'%n)
plt.tight_layout()
plt.show()
plt.pause(0.001)
# prochaine itération en raffinement
n = n+1
err = 0.0
# lboucle sur pixels blancs puis pixels noirs
for (i, j, k) in blanc+noir:
du = (u[i-1,j,k] + u[i+1,j,k] + u[i,j-1,k] + u[i,j+1,k] + u[i,j,k-1] \
+ u[i,j,k+1] + dx**2*rho[i,j,k])/6.0 - u[i,j,k]
u[i,j,k] += omega*du
err += abs(du)
err /= N**3
# tracé de surface de la solution finale
(x, y) = np.meshgrid(x, y)
s = s.clip(eps, 1.0)
levels = [10**(l/2.0) for l in range(-5, 0)]
fig = plt.figure()
axis = fig.gca(projection='3d', azim=-60, elev=20)
surf = axis.plot_surface(x, y, s.T, rstride=1, cstride=1, cmap='viridis')
wire = axis.plot_wireframe(x, y, s.T, rstride=1+N//50, cstride=1+N//50,
color = "r", linewidth=0.5, alpha = 0.5)
axis.contour(x, y, s.T, levels, zdir='z', offset=-1.0)
axis.contourf(x, y, s.T, 4, zdir='x', offset=-L)
axis.contourf(x, y, s.T, 4, zdir='y', offset=L)
axis.set_zlim(-1.0, 1.0)
axis.set_xlabel('x')
axis.set_ylabel('y')
axis.set_zlabel('u')
fig.colorbar(surf)
plt.tight_layout()
plt.savefig("charge.png"); plt.savefig("charge.pdf")
plt.show()
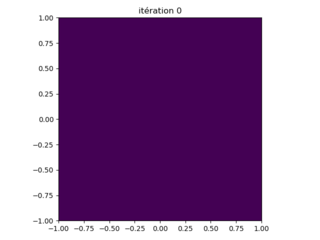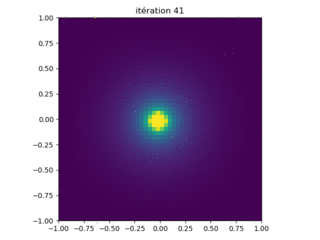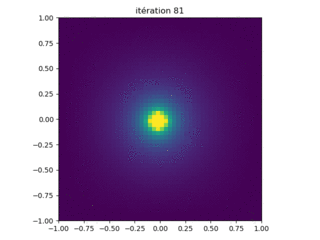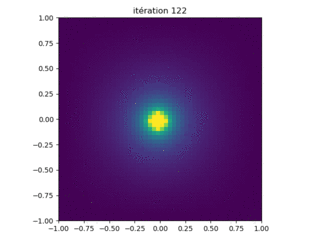
Figure 10: Résultats de l'exécution du programme charge.py avec des paramètres N = 50 points de grille le long de chaque côté.